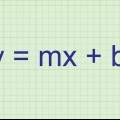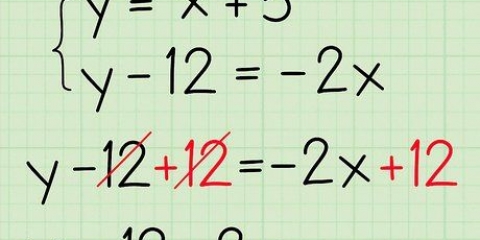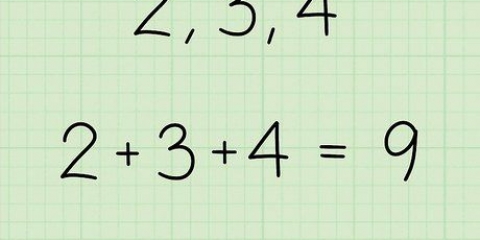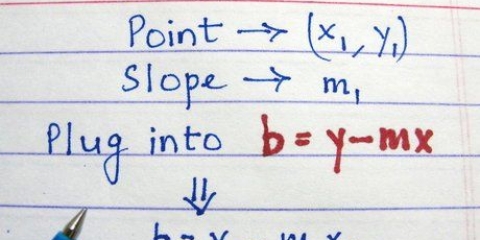(3-5)/(8-2) = -2/6 = -1/3 Die Steigung der Linie beträgt -1/3. Um diese Steigung zu finden, müssen Sie 2/6 auf den kleinsten Wert 1/3 vereinfachen, da sowohl 2 als auch 6 durch 2 . teilbar sind. 
Der negative Kehrwert von -1/3 ist 3, da 3/1 der Kehrwert von 1/3 ist und sich das Vorzeichen von negativ auf positiv geändert hat. 

3 --> y = mx + b = y = 3x + b 
(5, 4) --->y = 3x + b = 4 = 3(5) + b = 4 = 15 + b 
4 = 15 + b = -11 = b b = -11 
y = mx + b y = 3x - 11 Die Gleichung der Mittelsenkrechten durch die Punkte (2, 5) und (8, 3) ist y = 3 x - 11.
Bestimmung der mittelsenkrechten zweier punkte
Eine Mittelsenkrechte ist eine Linie, die ein Segment, das durch zwei Punkte in einem Winkel von 90 Grad verbunden ist, halbiert. Um die Mittelsenkrechte zweier Punkte zu finden, müssen Sie nur deren Mittelpunkte und den Kehrwert ermitteln und dann die Antworten auf die Gleichung einer Geraden der Form y = mx + b . anwenden. Wenn Sie wissen möchten, wie Sie die Mittelsenkrechte zweier Punkte finden, führen Sie die folgenden Schritte aus.
Schritte
Methode 1 von 2: Informationen sammeln

1. Finden Sie den Mittelpunkt der beiden Punkte. Ermitteln Sie den Mittelpunkt von zwei Punkten, indem Sie die Punkte auf die Mittelpunktsformel anwenden: [(X1 + x2)/2,( ja1 + ja2)/2]. Dies bedeutet, dass Sie die x- und y-Koordinaten der beiden Punkte mitteln, was Ihnen den Mittelpunkt der beiden Koordinaten ergibt. Angenommen, wir arbeiten mit den Koordinaten (x1, ja1) von (2, 5) und die Koordinaten (x2, ja2) von (8, 3). Den Mittelpunkt der beiden Punkte bestimmen Sie wie folgt:
- [(2+8)/2, (5 +3)/2] =
- (10/2, 8/2) =
- (5, 4)
- Die Koordinaten des Zentrums von (2, 5) und (8, 3) sind (5, 4).

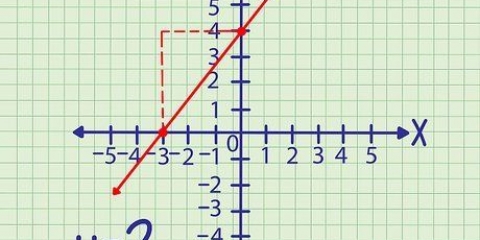
2. Finden Sie die Steigung der beiden Punkte. Um die Steigung (Steigung) der beiden Punkte zu ermitteln, wenden Sie die Punkte auf die Steigungsformel an: (ja2 - ja1) / (x2 - x1). Die Steigung einer Geraden ist der Abstand einer vertikalen Änderung über den Abstand einer entsprechenden horizontalen Änderung. Die Steigung der Geraden durch die Punkte (2, 5) und (8, 3) bestimmen Sie wie folgt:

3. Bestimmen Sie den negativen Kehrwert der Steigung der beiden Punkte. Um den negativen Kehrwert einer Steigung zu ermitteln, nehmen Sie den Kehrwert der Steigung und ändern Sie das Vorzeichen. Sie können den Kehrwert einer Zahl finden, indem Sie die x- und y-Koordinaten umkehren. Der negative Kehrwert von 1/2 ist -2/1 oder nur -2; der Kehrwert von -4 ist 1/4.
Methode 2 von 2: Berechnen Sie die Liniengleichung

1. Schreiben Sie die Geradengleichung in der Form y = mx + b. Die Gleichung einer Geraden durch zwei Punkte hat die Form `y = mx + b ` wobei die x- und y-Koordinaten auf der Linie durch `x` und `y` dargestellt werden, `m` steht für die Steigung der Linie und `b` steht für den Schnittpunkt der Linie mit der y-Achse. Sobald Sie diese Gleichung geschrieben haben, können Sie damit beginnen, die Gleichung der Mittelsenkrechten der beiden Punkte zu finden.

2. Wenden Sie den negativen Kehrwert der ursprünglichen Steigung auf die Gleichung an. Der negative Kehrwert der Steigung der Punkte (2, 5) und (8, 3) war 3. Das `m` in der Gleichung stellt die Steigung dar, also geben Sie 3 für das `m` in die Gleichung einer geraden Linie ein, y = mx + b.

3. Wenden Sie den Mittelpunkt auf die Linie an. Sie wissen bereits, dass die Mittelpunkte der Punkte (2, 5) und (8, 3) gleich (5, 4) sind. Da die Mittelsenkrechte durch die Mittelpunkte der beiden Geraden verlaufen, können Sie die Koordinaten der Mittelpunkte auf die Geradengleichung anwenden. Geben Sie einfach (5, 4) anstelle der x- und y-Koordinaten der Linie ein.

4. Nach dem Schnittpunkt auflösen. Sie haben drei der vier Variablen in der Geradengleichung gefunden. Jetzt haben Sie genügend Informationen, um die verbleibende Variable `b` zu bestimmen, den Schnittpunkt dieser Linie mit der y-Achse. Isolieren Sie die Variable `b`, um ihren Wert zu bestimmen. Subtrahiere 15 von beiden Seiten der Gleichung.

5. Schreiben Sie die Gleichung der Mittelsenkrechten. Um die Gleichung der Mittelsenkrechten zu schreiben, setzen Sie die Steigung der Geraden (3) und den Schnittpunkt mit der y-Achse (-11) in die Gleichung der Form y = mx + b . ein. Geben Sie nichts für die x- und y-Koordinaten ein, denn mit dieser Gleichung können Sie jede beliebige Koordinate auf der Linie finden, indem Sie eine x- oder eine y-Koordinate eingeben.
"Bestimmung der mittelsenkrechten zweier punkte"
Оцените, пожалуйста статью