Die Determinante einer 3x3-Matrix bestimmen

Schritte
- Teil 1 von 2: Bestimmung der Determinante
- Teil 2 von 2: Das Problem vereinfachen
Tipps

Die Determinante einer Matrix wird häufig in der Mathematik, der linearen Algebra und der höheren Geometrie verwendet. Außerhalb der wissenschaftlichen Welt verwenden Computergrafikingenieure und Programmierer häufig die Determinanten von Matrizen. Lesen Sie diesen Artikel, um die Determinante einer 3x3-Matrix zu bestimmen.

Schritte

Teil 1 von 2: Bestimmung der Determinante

Finden Sie die Determinante einer 3X3-Matrix Schritt 1

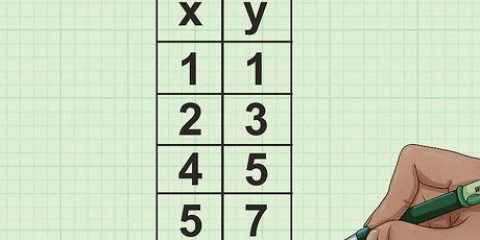
1. Schreiben Sie Ihre 3 x 3 Matrix auf. Wir beginnen mit einer 3 x 3 Matrix A und versuchen die Determinante |A| es mögen. Wir verwenden die folgende allgemeine Notation für die Matrix (und dies ist unsere Beispielmatrix):

$m = (\begin{matrix} ein \end{matrix} 11 {ein}_{12} {ein}_{13} {ein}_{21} & {ein}_{22} & {ein}_{23} {ein}_{31} & {ein}_{32} & {ein}_{33}) = (\begin{matrix} 1 & 5 & 3 \\ 2 & 4 & 7 \\ 4 & 6 & 2 \end{matrix})$ $M={begin{pmatrix}a_{{11}}&a_{{12}}&a_{{13}}\a_{{21}}&a_{{22}}&a_{ {23}}\a_{{31}}&a_{{32}}&a_{{33}}end{pmatrix}}={begin{pmatrix}1&5&3\2& 4&7\4&6&2end{pmatrix}}$

Finden Sie die Determinante einer 3X3-Matrix Schritt 2

2. Wählen Sie eine Zeile oder Spalte aus. Dies wird Ihre Referenzzeile oder -spalte sein. Sie erhalten die gleiche Antwort, egal für welche Sie sich entscheiden. Jetzt einfach die erste Reihe auswählen. Später beraten wir Sie, wie Sie die am einfachsten zu berechnende Option wählen können.

Wählen wir die erste Zeile unserer Beispielmatrix A. Kreisen Sie die 1 5 3 ein. Im Allgemeinen kreise a . ein₁₁ ein₁₂ ein₁₃.

Finden Sie die Determinante einer 3X3-Matrix Schritt 3

3. Streichen Sie die Zeile und Spalte des ersten Elements durch. Sehen Sie sich die eingekreiste Zeile oder Spalte an und wählen Sie das erste Element aus. Ziehen Sie eine Linie durch die entsprechende Zeile und Spalte. Wenn alles gut geht, ergeben sich jetzt vier Zahlen. Wir behandeln dies als 2 x 2 Matrix.

In unserem Beispiel ist die Referenzzeile 1 5 3. Es erstes Element ist in Zeile 1 und Spalte 1. Zeile 1 und Spalte 1 komplett durchstreichen. Notieren Sie die restlichen Elemente als a2 x 2 Matrix:

~~1 5 3~~
2 4 7
4 6 2

Finden Sie die Determinante einer 3X3-Matrix Schritt 4

4. Bestimmen Sie die Determinante der 2 x 2 Matrix. Nicht vergessen: die Matrix

(\begin{matrix} ein & B \\ C & D \end{matrix})

${begin{pmatrix}a&b\c&dend{pmatrix}}$ hat eine Determinante von ad - bc. Sie wissen dies, indem Sie ein Kreuz (X) durch die 2 x 2-Matrix ziehen. Multiplizieren Sie die beiden Zahlen, die mit dem von X . verbunden sind. Subtrahiere dann das Produkt der beiden Zahlen, die durch / verbunden sind. Verwenden Sie diese Formel, um die Determinante der gerade gefundenen Matrix zu berechnen.

In unserem Beispiel ist die Determinante der Matrix

(\begin{matrix} 4 & 7 \\ 6 & 2 \end{matrix})

${begin{pmatrix}4&7\6&2end{pmatrix}}$ = 4 * 2 - 7 * 6 = -34.

Diese Determinante heißt unerheblich des Elements, das wir in unserer ursprünglichen Matrix ausgewählt haben. In diesem Fall haben wir den Minderjährigen von ein₁₁ fand es.

Finden Sie die Determinante einer 3X3-Matrix Schritt 5

5. Multiplizieren Sie die Antwort mit Ihrem gewählten Element. Denken Sie daran, dass Sie ein Element aus Ihrer Referenzzeile (oder -spalte) ausgewählt haben, als Sie entschieden haben, welche Zeile und Spalte Sie durchstreichen möchten. Multiplizieren Sie dieses Element mit der Determinante, die Sie gerade für die 2x2-Matrix berechnet haben.

In unserem Beispiel haben wir a₁₁ ausgewählt, die einen Wert von 1 . hat. Multiplizieren Sie dies mit -34 (der Determinante der 2x2-Matrix), um 1*-34 = . zu erhalten -34 bekommen.

Finden Sie die Determinante einer 3X3-Matrix Schritt 6

6. Bestimmen Sie das Vorzeichen Ihrer Antwort. Multiplizieren Sie nun die Antwort mit 1 oder mit -1, um das zu erhalten Cofaktor Ihres gewählten Elements. Welche Sie verwenden, hängt von der Position des Elements in der 3x3-Matrix ab. Merken Sie sich die folgende einfache Tabelle, um herauszufinden, welches Element was bewirkt:

+ - +
- + -
+ - +

Weil wir ein₁₁ gewählt haben, mit einem + markiert, multiplizieren wir die Zahl mit +1 (d.h. wir machen nichts damit). Die Antwort ist immer noch -34.

Eine andere Möglichkeit, das Vorzeichen zu bestimmen, ist die Formel (-1), wobei ich und J Bilde die Zeile und Spalte des Elements.

Finden Sie die Determinante einer 3X3-Matrix Schritt 7

7. Wiederholen Sie diesen Vorgang für das zweite Element in Ihrer Referenzzeile oder -spalte. Fahren Sie mit der ursprünglichen 3x3-Matrix fort, mit der Zeile oder Spalte, die Sie zuvor eingekreist haben. Wiederholen Sie den gleichen Vorgang mit diesem Element:

Überqueren Sie die Zeile und Spalte dieses Elements. In diesem Fall wählen Sie das Element a₁₂ (mit Wert 5). Überqueren Sie die erste Reihe (1 5 3) und die zweite Spalte

(\begin{matrix} 5 \\ 4 \\ 6 \end{matrix})

${begin{pmatrix}5\4\6end{pmatrix}}$ .

Behandeln Sie die restlichen Elemente als 2x2-Matrix. In unserem Beispiel ist die Matrix

(\begin{matrix} 2 & 7 \\ 4 & 2 \end{matrix})

${begin{pmatrix}2&7\4&2end{pmatrix}}$

Bestimmen Sie die Determinante dieser 2x2-Matrix. Verwenden Sie die Formel ad - bc. (2*2 - 7*4 = -24)

Multiplizieren Sie dies mit dem gewählten Element der 3x3-Matrix. -24 * 5 = -120

Bestimmen Sie, ob mit -1 . multipliziert werden soll. Verwenden Sie die Zeichentabelle oder die Formel (-1). Wir haben Element a₁₂ gewählt, und das ist ein – auf der Zeichentabelle. Wir müssen das Vorzeichen unserer Antwort ändern: (-1)*(-120) = 120.

Finden Sie die Determinante einer 3X3-Matrix Schritt 8

8. Wiederholen Sie dies für das dritte Element. Du musst jetzt einen Cofaktor finden. Berechnen Sie i für den dritten Term in Ihrer Referenzzeile oder -spalte. Hier ist eine kurze Erklärung zur Berechnung des Kofaktors von ₁₃ in unserem Beispiel:

Überqueren Sie Zeile 1 und Spalte 3 und erhalten Sie

(\begin{matrix} 2 & 4 \\ 4 & 6 \end{matrix})

${begin{pmatrix}2&4\4&6end{pmatrix}}$

Seine Determinante ist 2*6 - 4*4 = -4.

Multiplizieren Sie dies mit dem Element a₁₃: -4 * 3 = -12.

Element a₁₃ ist ein + in der Zeichentabelle, also lautet die Antwort -12.

Finden Sie die Determinante einer 3X3-Matrix Schritt 9

9. Addiere die drei Ergebnisse zusammen. Dies ist der letzte Schritt. Sie haben Kofaktoren berechnet, einen für jedes Element in einer einzelnen Zeile oder Spalte. Addiere diese zusammen und du hast die Determinante der 3x3-Matrix gefunden.

In unserem Beispiel ist die Determinante -34 + 120 + -12 = 74.

Teil 2 von 2: Das Problem vereinfachen

Finden Sie die Determinante einer 3X3-Matrix Schritt 10

1. Wählen Sie die Referenz mit den meisten Nullen. Vergiss nicht, dass du jeder kann Zeile oder Spalte als Referenz wählen. Sie erhalten die gleiche Antwort, egal wofür Sie sich entscheiden. Wenn Sie eine Zeile oder Spalte mit Nullen wählen, müssen Sie nur den Kofaktor der Elemente berechnen, die nicht Null sind. Der Grund ist folgender:

Angenommen, Sie wählen Zeile 2 mit den Elementen a₂₁, ein₂₂, und ein₂₃. Um dieses Problem zu lösen, betrachten wir drei verschiedene 2x2-Matrizen. Angenommen, wir nennen dies A₂₁, ein₂₂ und ein₂₃.
Die Determinante der 3x3-Matrix ist a₂₁|A₂₁| - ein₂₂|A₂₂| + a₂₃|A₂₃|.
Wenn die Begriffe a₂₂ und ein₂₃ sind beide 0, dann wird unsere Formel₂₁|A₂₁| - 0*|A₂₂| + 0*|A₂₃| = a₂₁|A₂₁| - 0 + 0 = a₂₁|A₂₁|. Jetzt müssen wir nur noch den Kofaktor eines einzelnen Elements berechnen.

Finden Sie die Determinante einer 3X3-Matrix Schritt 11

2. Fügen Sie die Zeilen zusammen, um die Matrix zu vereinfachen. Wenn Sie die Werte einer Zeile nehmen und zu einer anderen hinzufügen, ändert sich die Determinante der Matrix nicht. Das gleiche gilt für Spalten. Sie können dies wiederholt tun – oder die Werte vor dem Addieren mit einer Konstanten multiplizieren – um so viele Nullen wie möglich in der Matrix zu erhalten. Das kann dir viel Arbeit ersparen.

Angenommen, Sie haben eine 3x3-Matrix:

(\begin{matrix} 9 & - 1 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}9&-1&2\3&1&0\7&5&-2end{pmatrix}}$

Alle 9 in Position a₁₁ Um es loszuwerden, können wir die zweite Zeile mit -3 multiplizieren und das Ergebnis zur ersten addieren. Die neue erste Zeile wird dann [9 -1 2] + [-9 -3 0] = [0 -4 2].

Die neue Matrix ist

(\begin{matrix} 0 & - 4 & 2 \\ 3 & 1 & 0 \\ 7 & 5 & - 2 \end{matrix})

${begin{pmatrix}0&-4&2\3&1&0\7&5&-2end{pmatrix}}$ Versuchen Sie, den gleichen Trick für die Spalten anzuwenden, um₁₂ eine 0 machen.

Finden Sie die Determinante einer 3X3-Matrix Schritt 12

3. Lerne den Trick zum Lösen von Dreiecksmatrizen. In diesen Spezialfällen ist die Determinante einfach das Produkt der Elemente entlang der Hauptdiagonalen von a₁₁ oben links nach a₃₃ unten rechts. Wir sprechen immer noch von 3x3-Matrizen, aber `dreieckige` Matrizen haben spezielle Wertemuster, die nicht null sind:

Obere Dreiecksmatrix: Alle Nicht-Null-Elemente befinden sich auf oder über der Hauptdiagonalen. Alle Werte darunter sind Null.

Untere Dreiecksmatrix: Alle Nicht-Null-Elemente befinden sich auf oder unter der Hauptdiagonale.

Diagonalmatrix: Alle von Null verschiedenen Elemente befinden sich auf der Hauptdiagonalen. (Eine Teilmenge der oben genannten.)

Tipps

Diese Methode kann für quadratische Matrizen jeder Größe verwendet werden. Wenn Sie dies beispielsweise für eine 4x4-Matrix verwenden, behalten Sie nach dem "streichen" eine 3x3-Matrix, für die Sie die Determinante wie oben angegeben berechnen können. Seien Sie gewarnt, denn dies von Hand zu tun wird sehr langweilig!
Wenn alle Elemente einer Zeile oder Spalte gleich 0 sind, dann ist die Determinante dieser Matrix gleich 0.