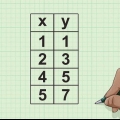
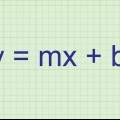Beispiel: Sie haben ein Dreieck mit einer Grundfläche von 15 Zentimetern und ein entsprechendes Dreieck mit einer Grundfläche von 10 cm Länge. 
Wenn Sie beispielsweise ein Dreieck mit einer Grundfläche von 15 cm auf ein Dreieck mit einer Grundfläche von 10 cm reduzieren, ist das Verhältnis  .
.
Durch Eingabe der richtigen Werte wird dies zu .
. 
Zum Beispiel: das Verhältnis  kann vereinfacht werden zu
kann vereinfacht werden zu . Der Skalierungsfaktor von zwei Dreiecken, eines mit einer Basis von 15 cm und eines mit einer Basis von 10 cm, ist also
. Der Skalierungsfaktor von zwei Dreiecken, eines mit einer Basis von 15 cm und eines mit einer Basis von 10 cm, ist also  .
. 

Mit einem Skalierungsfaktor von 2 vergrößern Sie beispielsweise die Abbildung. 
Wenn beispielsweise die Hypotenuse eines rechtwinkligen Dreiecks 5 Zentimeter lang ist und der Skalierungsfaktor 2 beträgt, berechnen Sie zur Bestimmung der Hypotenuse des entsprechenden Dreiecks  . Das skalierte Dreieck hat also eine Hypotenuse von 10 cm.
. Das skalierte Dreieck hat also eine Hypotenuse von 10 cm. 
Wenn beispielsweise die Basis eines rechtwinkligen Dreiecks 3 cm beträgt, berechnen Sie mit einem Skalierungsfaktor von 2  für die Basis des skalierten Dreiecks. Wenn die Höhe eines rechtwinkligen Dreiecks 4 cm lang ist, mit einem Skalierungsfaktor von 2, dann berechnen Sie
für die Basis des skalierten Dreiecks. Wenn die Höhe eines rechtwinkligen Dreiecks 4 cm lang ist, mit einem Skalierungsfaktor von 2, dann berechnen Sie  für die Höhe des skalierten Dreiecks.
für die Höhe des skalierten Dreiecks. 

Unregelmäßige Figuren können skaliert werden, wenn ihre Seiten alle proportional sind. So können Sie einen Skalierungsfaktor mit jeder gegebenen Größe berechnen. Da Sie die Breite jedes Polygons kennen, können Sie eine Verhältnisgleichung aufstellen. Wenn Sie das Verhältnis erhöhen, verwenden Sie  . Wenn Sie reduzieren möchten, verwenden Sie das Verhältnis
. Wenn Sie reduzieren möchten, verwenden Sie das Verhältnis  .
. Vereinfachen Sie das Verhältnis. Das Verhältnis  kann vereinfacht werden zu
kann vereinfacht werden zu  . Das Verhältnis
. Das Verhältnis  kann vereinfacht werden zu
kann vereinfacht werden zu  . Die beiden unregelmäßigen Polygone haben also einen Skalierungsfaktor von
. Die beiden unregelmäßigen Polygone haben also einen Skalierungsfaktor von  oder
oder  .
. 
Multiplizieren Sie die Höhe des Rechtecks ABCD mit dem Skalierungsfaktor. Dadurch erhalten Sie die Höhe des Rechtecks EFGH:  .
. Multiplizieren Sie die Breite des Rechtecks ABCD mit dem Skalierungsfaktor. Dies gibt Ihnen die Breite des Rechtecks EFGH:  .
. Multiplizieren Sie die Höhe und Breite des Rechtecks EFGH für die Fläche:  . Die Fläche des Rechtecks EFGH beträgt also 150 cm2.
. Die Fläche des Rechtecks EFGH beträgt also 150 cm2. 

Beispiel: Um die Summenformel des betreffenden Stoffes zu bestimmen, multiplizieren Sie den Index von H2O mit dem Skalierungsfaktor 3. H2O * 3 = H6O3 
Beispiel: Der Skalierungsfaktor für die Verbindung beträgt 3. Die Summenformel der Substanz lautet H6O3.
Bestimmung des skalierungsfaktors
Der (lineare) Skalierungsfaktor ist das Verhältnis zweier korrespondierender Seiten von Figuren gleicher Form. Ähnliche Figuren haben die gleiche Form, aber unterschiedliche Größen. Der Skalierungsfaktor wird verwendet, um einfache geometrische Probleme zu lösen. Mit dem Skalierungsfaktor können Sie die unbekannten Seiten einer Figur bestimmen. Umgekehrt können Sie die Seitenlänge zweier ähnlicher Zahlen verwenden, um den Skalierungsfaktor zu berechnen. Bei solchen Problemen müssen Sie Brüche multiplizieren oder vereinfachen.
Schritte
Methode 1 von 4: Bestimmung des Skalierungsfaktors einer skalierten Figur

1. Überprüfen Sie, ob die Zahlen ähnlich sind. Figuren gleicher Form haben die gleichen Winkel und die Seitenlängen sind proportional. Ähnliche Figuren haben die gleiche Form, aber eine Figur ist größer als die andere.
- Die Aussage muss angeben, dass die Formen gleich sind oder zeigen, dass die Winkel gleich sind, andernfalls angeben, dass das Längenverhältnis der Seiten proportional, maßstabsgetreu ist oder dass sie einander entsprechen.

2. Finden Sie eine passende Seite jeder Figur. Möglicherweise müssen Sie die Figur drehen oder spiegeln, damit die beiden Formen ausgerichtet sind und Sie die entsprechenden Seiten erkennen. Die Länge dieser beiden Seiten muss angegeben werden, oder Sie müssen sie messen können. Wenn keine Seitenlänge jeder Figur bekannt ist, können Sie den Skalierungsfaktor nicht finden.

3. Stellen Sie das Verhältnis fest. Für jedes Paar übereinstimmender Figuren gibt es zwei Skalierungsfaktoren: einen beim Vergrößern einer Figur und einen beim Verkleinern. Wenn Sie auf eine größere Version vergrößern, verwenden Sie das Verhältnis  . Verwenden Sie beim Ändern der Größe einer Figur das Verhältnis
. Verwenden Sie beim Ändern der Größe einer Figur das Verhältnis  .
.
 . Verwenden Sie beim Ändern der Größe einer Figur das Verhältnis
. Verwenden Sie beim Ändern der Größe einer Figur das Verhältnis  .
. .
.Durch Eingabe der richtigen Werte wird dies zu
 .
.
4. Vereinfachen Sie das Verhältnis. Das vereinfachte Verhältnis oder der Bruch gibt Ihnen den Skalierungsfaktor. Wenn Sie den Skalierungsfaktor reduzieren, wird ein regulärer Bruchteil. Wenn Sie es vergrößern, wird es eine ganze Zahl oder ein unechter Bruch, den Sie in eine Dezimalzahl umwandeln können.
 kann vereinfacht werden zu
kann vereinfacht werden zu . Der Skalierungsfaktor von zwei Dreiecken, eines mit einer Basis von 15 cm und eines mit einer Basis von 10 cm, ist also
. Der Skalierungsfaktor von zwei Dreiecken, eines mit einer Basis von 15 cm und eines mit einer Basis von 10 cm, ist also  .
.Methode 2 von 4: Ermittlung einer entsprechenden Zahl mit Hilfe des Skalierungsfaktors

1. Bestimmen Sie die Länge der Seite der Figur. Sie brauchen eine Figur, deren Seiten vorgegeben oder messbar sind. Wenn Sie die Seitenlänge des Bildes nicht bestimmen können, können Sie keine skalierte Figur erstellen.
- Beispiel: Sie haben ein rechtwinkliges Dreieck mit Seitenlängen von 4 cm und 3 cm und einer Hypotenuse von 5 cm.

2. Entscheiden Sie, ob Sie vergrößern oder verkleinern möchten. Wenn Sie vergrößern, wird Ihre fehlende Zahl größer und der Skalierungsfaktor ist eine ganze Zahl, ein unechter Bruch oder eine Dezimalzahl. Wenn Sie schrumpfen, wird die Zahl kleiner und Ihr Skalierungsfaktor ist höchstwahrscheinlich ein regelmäßiger Bruch.

3. Multiplizieren Sie die Länge einer Seite mit dem Skalierungsfaktor. Der Skalierungsfaktor muss angegeben werden. Die Multiplikation der Seitenlänge mit dem Skalierungsfaktor ergibt die fehlende Seite der skalierten Figur.
 . Das skalierte Dreieck hat also eine Hypotenuse von 10 cm.
. Das skalierte Dreieck hat also eine Hypotenuse von 10 cm.
4. Bestimmen Sie die anderen Seiten der Figur. Fahren Sie fort, jede Seite mit dem Skalierungsfaktor zu multiplizieren. Dadurch erhalten Sie die entsprechenden Seiten der fehlenden Figur.
 für die Basis des skalierten Dreiecks. Wenn die Höhe eines rechtwinkligen Dreiecks 4 cm lang ist, mit einem Skalierungsfaktor von 2, dann berechnen Sie
für die Basis des skalierten Dreiecks. Wenn die Höhe eines rechtwinkligen Dreiecks 4 cm lang ist, mit einem Skalierungsfaktor von 2, dann berechnen Sie  für die Höhe des skalierten Dreiecks.
für die Höhe des skalierten Dreiecks.Methode 3 von 4: Einige Beispielübungen

1. Bestimmen Sie den Skalierungsfaktor dieser entsprechenden Zahlen: ein Rechteck mit einer Höhe von 6 cm und ein Rechteck mit einer Höhe von 54 cm.
- Vergleichen Sie die beiden Höhen. Um zu erhöhen, ist das Verhältnis
. Verwenden Sie zum Verkleinern das Verhältnis
.
- Vereinfachen Sie das Verhältnis. Das Verhältnis
kann vereinfacht werden zu
. Das Verhältnis
kann vereinfacht werden zu
. Die beiden Rechtecke haben also einen Skalierungsfaktor von
oder
.

2. Versuchen Sie die folgende Aufgabe. Ein unregelmäßiges Vieleck ist an seiner breitesten Stelle 14 cm lang. Ein entsprechendes unregelmäßiges Polygon ist an der breitesten Stelle 8 cm. Was ist der Skalierungsfaktor?
 . Wenn Sie reduzieren möchten, verwenden Sie das Verhältnis
. Wenn Sie reduzieren möchten, verwenden Sie das Verhältnis  .
. kann vereinfacht werden zu
kann vereinfacht werden zu  . Das Verhältnis
. Das Verhältnis  kann vereinfacht werden zu
kann vereinfacht werden zu  . Die beiden unregelmäßigen Polygone haben also einen Skalierungsfaktor von
. Die beiden unregelmäßigen Polygone haben also einen Skalierungsfaktor von  oder
oder  .
.
3. Verwenden Sie den Skalierungsfaktor, um das folgende Problem zu beantworten. Rechteck ABCD ist 8 cm x 3 cm. Rechteck EFGH ist ein größeres entsprechendes Rechteck. Gegeben ist ein Skalierungsfaktor von 2.5. Was ist die Fläche des Rechtecks EFGH?
 .
. .
. . Die Fläche des Rechtecks EFGH beträgt also 150 cm2.
. Die Fläche des Rechtecks EFGH beträgt also 150 cm2.Methode 4 von 4: Der Skalierungsfaktor in der Chemie

1. Teilen Sie die Molmasse eines Stoffes durch die der Summenformel. Wenn Sie die Summenformel einer chemischen Verbindung kennen und die Summenformel derselben Chemikalie benötigen, können Sie den benötigten Skalierungsfaktor finden, indem Sie die Molmasse der Substanz durch die Molmasse der Summenformel dividieren.
- Beispiel: Sie möchten die Molmasse einer H2O-Verbindung mit einer Molmasse von 54,05 g/mol . wissen.
- Die Molmasse von H2O beträgt 18.0152 g/mol.
- Bestimmen Sie den Skalierungsfaktor, indem Sie die Molmasse der Verbindung durch die Molmasse der Summenformel teilen:
- Skalierungsfaktor = 54,05 / 18,0152 = 3

2. Multiplizieren Sie die empirische Formel mit dem Skalierungsfaktor. Multiplizieren Sie den Index jedes Elements innerhalb der empirischen Formel mit dem Skalierungsfaktor, den Sie gerade berechnet haben. Dadurch erhalten Sie die Summenformel der Verbindung.

3. Schreibe die Antwort auf. Mit dieser Antwort haben Sie die richtige Antwort für die Summenformel sowie die Summenformel der chemischen Bindung gefunden.
Оцените, пожалуйста статью