Beträgt das experimentelle Maß 60 cm, muss die Berechnung der Ungenauigkeit auch auf eine ganze Zahl gerundet werden. Die Ungenauigkeit dieser Messung kann beispielsweise 60 cm ± 2 cm betragen, jedoch nicht 60 cm ± 2 Zoll.2 cm². Wenn Ihr experimenteller Messwert 3 . beträgt.4 cm, dann muss die Ungenauigkeit ebenfalls auf 0,1 cm . gerundet werden. Die Ungenauigkeit dieser Messung kann beispielsweise 3 . betragen.4cm ± .1 cm sein, aber nicht 3.4cm ± 1cm. 
Schauen Sie sich die Kugelkante und das Lineal genau an, um eine Vorstellung davon zu bekommen, wie zuverlässig Ihre Messung sein kann. In einem Standardlineal sind die 0,5-cm-Markierungen deutlich markiert – aber angenommen, Sie können etwas näher herangehen. Wenn es so aussieht, als ob Sie mit Ihrer Messung innerhalb von 0,3 cm kommen können, beträgt die Ungenauigkeit 0,3 cm. Jetzt messen wir den Durchmesser der Kugel. Angenommen, Sie erhalten 7,6 cm als Antwort. Schreiben Sie nun die geschätzte Messung mit der Ungenauigkeit auf. Der Durchmesser der Kugel beträgt 7,6 cm ± 0,3 cm. 
Angenommen, Sie können mit einem normalen Lineal nicht viel näher als 0,2 cm herankommen. Die Ungenauigkeit beträgt also ± 0,2 cm. Angenommen, Sie haben gemessen, dass der Stapel der Kisten zusammen 22 cm² groß ist. Jetzt müssen Sie nur noch diesen Messwert und die Ungenauigkeit durch 10 (die Anzahl der Kästchen) dividieren. 22 cm/10 = 2,2 cm und 0,2 cm/10 = 0,02 cm. Dies bedeutet, dass die Dicke einer Schachtel 2,20 cm ± 0,02 cm² beträgt. 



0,43 s – 0,42 s = 0,01 s 0,52s - 0,42s = 0,1s 0,35 s - 0,42 s = -0,07 s 0,29 s - 0,42 s = -0,13 s 0,49 s - 0,42 s = 0,07 s Addiere nun die Quadrate der Differenzen: (0,01 s) + (0,1 s) + (-0,07 s) + (-0,13 s) +(0,07 s)= 0,037 s. Ermitteln Sie den Mittelwert dieser addierten Quadrate, indem Sie das Ergebnis durch 5 . dividieren. 0,037 s/5 = 0,0074 s. 



(10cm ± .4cm) - (3cm ± .2cm) = (10cm - 3cm) ± (.4 cm +. 2cm) = 7cm ± 0,6cm (6 cm ± 0,2 cm) = (0,2 / 6) x 100 und füge ein %-Zeichen hinzu. Das sind 3,3%
Daher:
(6 cm ± 0,2 cm) x (4 cm ± 0,3 cm) = (6 cm ± 3,3%) x (4 cm ± 7,5%) (6cm x 4cm) ± (3.3 + 7,5) = 24 cm ± 10,8% = 24 cm ± 2,6 cm (10 cm ± 0,6 cm) ÷ (5 cm ± 0,2 cm) = (10 cm ± 6 %) ÷ (5 cm ± 4 %) (10 cm ÷ 5 cm) ± (6% + 4%) = 2 cm ± 10 % = 2 cm ± 0,2 cm 
(2,0 cm ± 1.0cm) = (2,0 cm) ± (1,0 cm) x 3 = 8,0 cm ± 3 cm
Ungenauigkeit berechnen
Wenn Sie während der Datenerhebung eine Messung durchführen, können Sie davon ausgehen, dass "echter Wert" liegt im Bereich der von Ihnen vorgenommenen Messungen. Wenn Sie die Ungenauigkeit Ihrer Messwerte berechnen möchten, müssen Sie den besten Schätzwert Ihrer Messwerte ermitteln und diesen beim Subtrahieren oder Addieren der Messwertungenauigkeit berücksichtigen.
Schritte
Methode 1 von 3: Erlernen der Grundlagen

1. Bestimmen Sie die richtige Form für Ungenauigkeiten. Angenommen, Sie messen die Länge eines Stäbchens von etwa 4,2 cm mit einem Rand von 1 Millimeter. Dies bedeutet, dass der Stick mit ziemlicher Sicherheit 4,2 cm groß ist, aber etwas größer oder kleiner als diese Länge sein kann, mit einer Fehlertoleranz von 1 Millimeter.
- Notieren Sie dies wie folgt: 4,2 cm ± 0,1 cm. Sie können dies umschreiben als: 4,2 cm ± 1 mm, denn 0,1 cm = 1 mm.

2. Runden Sie den experimentellen Messwert auf die gleiche Anzahl von Dezimalstellen wie die Ungenauigkeit. Messungen mit Ungenauigkeiten werden normalerweise auf 1 oder 2 signifikante Zahlen gerundet. Der entscheidende Punkt ist, dass Sie die Messungen des Experiments auf die gleiche Anzahl von Dezimalstellen wie die Ungenauigkeit runden, um die Messungen konsistent zu halten.

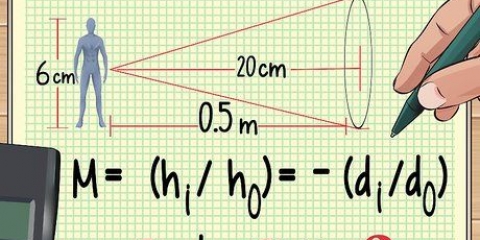
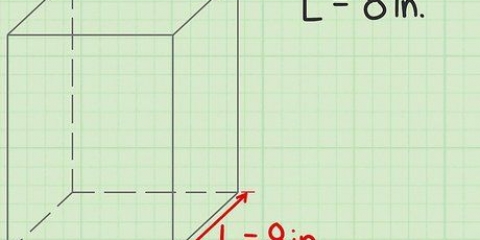
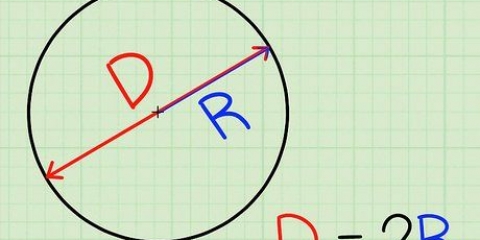
3. Berechnen Sie die Ungenauigkeit einer einzelnen Messung. Angenommen, Sie messen den Durchmesser einer runden Kugel mit einem Lineal. Dies ist schwierig, da es schwierig ist, genau zu bestimmen, wo sich die Außenkante der Kugel befindet und wie man sie mit dem Lineal misst. Angenommen, das Lineal kann den Durchmesser mit einer Genauigkeit von 0,1 cm ermitteln - das bedeutet nicht, dass Sie den Durchmesser der Kugel mit dieser Genauigkeit messen können.

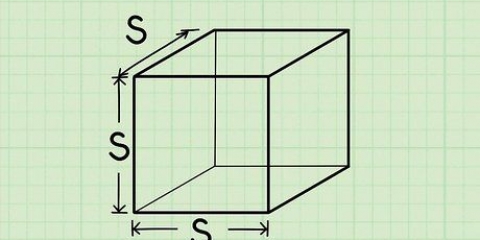
4. Berechnen Sie die Ungenauigkeit einer einzelnen Messung mehrerer Objekte. Angenommen, Sie messen die Höhe eines Stapels von 10 CD-Hüllen, die alle Abmessungen haben. Angenommen, Sie möchten wissen, wie dick 1 Schachtel ist. Dieser Messwert ist so gering, dass der Prozentsatz der Ungenauigkeit hoch ist. Aber wenn Sie 10 Boxen messen, können Sie das Ergebnis teilen und einfach seine Ungenauigkeit durch die Anzahl der Boxen im Stapel dividieren, um die Dicke von 1 Box zu ermitteln.

5. Führen Sie diese Messung mehrmals durch. Um die Genauigkeit Ihrer Messung zu erhöhen, egal ob Sie die Länge eines Objekts messen oder die Zeit, die zum Zurücklegen einer bestimmten Distanz benötigt wird, erhöhen Sie die Wahrscheinlichkeit einer genauen Messung, wenn Sie mehrere Messungen durchführen. Die Ermittlung des Durchschnitts aller Messungen führt letztendlich zu einer besseren Bestimmung der Ungenauigkeit einer Messung.
Methode 2 von 3: Berechnung der Ungenauigkeit mehrerer Messungen

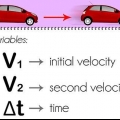
1. Nehmen Sie mehrere Messungen vor. Angenommen, Sie möchten berechnen, wie lange es dauert, bis ein Ball vom Tisch auf die Runde fällt. Um die besten Ergebnisse zu erzielen, müssen Sie dieselbe Messung mindestens einige Male durchführen – sagen wir, wir machen dies fünfmal. Dann müssen Sie den Mittelwert dieser 5 Messungen berechnen und dann die Standardabweichung davon addieren oder subtrahieren, um das beste Ergebnis zu erhalten.
- Angenommen, Sie haben die folgenden Messwerte: 0,43 s, 0,52 s, 0,35 s, 0,29 s und 0,49 s.

2. Bestimmen Sie den Durchschnitt der Messungen. Sie tun dies, indem Sie alle fünf zusammenzählen und die Summe durch 5 teilen, die Anzahl der Messwerte. 0,43 s + 0,52 s + 0,35 s + 0,29 s + 0,49 s = 2.08 s. Jetzt teilen 2.08 von 5. 2.08/5 = 0,42 Sek. Der Mittelwert beträgt 0,42 s.

3. Bestimmen Sie die Varianz dieser Messungen. Sie tun dies, indem Sie die Differenz zwischen jeder der 5 Messungen und dem Durchschnitt bestimmen. Subtrahiere die Messwerte von 0,42 s. Hier sind die 5 Unterschiede:

4. Bestimmen Sie die Standardabweichung. Dies kann durch Berechnung der Quadratwurzel der Varianz ermittelt werden. Das Quadrat von 0,0074 s = 0,09 s, die Standardabweichung beträgt also 0,09 s.

5. Geben Sie den endgültigen Messwert an. Sie tun dies, indem Sie den Mittelwert der gemessenen Werte zusammen mit der addierten und subtrahierten Standardabweichung notieren. Da der Mittelwert der Messwerte 0,42 s beträgt und die Standardabweichung 0,09 s beträgt, beträgt der endgültige Messwert 0,42 s ± 0,09 s.
Methode 3 von 3: Arithmetische Operationen mit Ungenauigkeit

1. Ungenauigkeit hinzufügen. Sie tun dies, indem Sie die Messwerte addieren und ihre Ungenauigkeiten hinzufügen:
- (5cm ± .2cm) + (3cm ± .1cm) =
- (5cm + 3cm) ± (.2 cm² +. 1cm) =
- 8cm ± .3 cm²

2. Ungenauigkeit abziehen. Sie tun dies, indem Sie die gemessenen Werte subtrahieren und die Ungenauigkeiten addieren:
3. Multiplikationsungenauigkeit.
Um die Ungenauigkeit zu multiplizieren, multiplizieren Sie die Messungen und addieren Sie die RELATIVE Ungenauigkeit (in Prozent):
Das Berechnen von Ungenauigkeiten durch Multiplikation funktioniert nicht mit absoluten Werten (wie bei Addition und Subtraktion), wohl aber mit relativen Werten. Sie erhalten die relative Ungenauigkeit, indem Sie die absolute Ungenauigkeit durch den gemessenen Wert dividieren und dann mit 100 . multiplizieren.
Zum Beispiel:
Um die Ungenauigkeit zu multiplizieren, multiplizieren Sie die Messungen und addieren Sie die RELATIVE Ungenauigkeit (in Prozent):
Das Berechnen von Ungenauigkeiten durch Multiplikation funktioniert nicht mit absoluten Werten (wie bei Addition und Subtraktion), wohl aber mit relativen Werten. Sie erhalten die relative Ungenauigkeit, indem Sie die absolute Ungenauigkeit durch den gemessenen Wert dividieren und dann mit 100 . multiplizieren.
Zum Beispiel:
Daher:
4. Ungenauigkeit beim Teilen.
Um die Ungenauigkeit zu teilen, teilen Sie die Messungen und addieren Sie die RELATIVE Ungenauigkeit:
Dieses Verfahren entspricht einer Multiplikation!
Um die Ungenauigkeit zu teilen, teilen Sie die Messungen und addieren Sie die RELATIVE Ungenauigkeit:
Dieses Verfahren entspricht einer Multiplikation!

5. Ungenaues Lesen exponentiell erhöhen. Um eine ungenaue Messung exponentiell zu erhöhen, erhöhen Sie die Messung um eine bestimmte Potenz und multiplizieren Sie dann die Ungenauigkeit mit dieser Potenz:
Tipps
- Sie können die Ergebnisse und die Standardungenauigkeit insgesamt oder für jedes Ergebnis innerhalb eines Datensatzes anzeigen. Als allgemeine Regel gilt, dass Daten aus mehreren Messungen weniger genau sind als direkt aus einer einzelnen Messung.
Warnungen
- Die hier beschriebene Ungenauigkeit gilt nur für die Fälle, in denen normale (Gaußsche, glockenförmige) Statistik verwendet wird. Andere Spreads erfordern eine andere Methode zur Beschreibung von Ungenauigkeiten.
- Gute Forschung endet nie "Fakten" oder was "wahr" ist. Obwohl eine Messung sehr wahrscheinlich in einen bestimmten Bereich von Ungenauigkeiten fällt, gibt es keine Garantie dafür, dass dies der Fall ist. Es ist wissenschaftlichen Messwerten inhärent, dass die Möglichkeit besteht, dass Messwerte falsch sind.
Оцените, пожалуйста статью