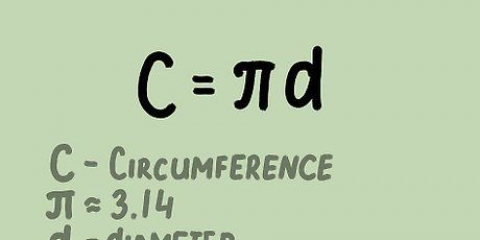Selbst die π-Taste eines Taschenrechners verwendet nicht den genauen Wert von π, obwohl er genau genug ist. 
C ist nur eine kürzere Schreibweise für "Umfang". 
Du hast die linke Seite vielleicht geschrieben als π2r, was auch richtig ist. Die Leute setzen gerne die Zahlen vor die Symbole, um die Gleichung besser lesbar zu machen, aber das ändert nichts am Ergebnis der Gleichung. In einer mathematischen Gleichung können Sie die linke und rechte Seite immer mit dem gleichen Betrag multiplizieren und erhalten trotzdem eine korrekte Gleichung. 
Wenn der Radius beispielsweise zwei Einheiten lang ist, dann ist 2πr = 2 x (3.14) x (2 Einheiten) = 12.56 Einheiten = der Umfang. Im gleichen Beispiel, aber mit der π-Taste eines Taschenrechners für eine bessere Genauigkeit, erhalten Sie 2 x π x 2 Einheiten = 12,56637... Einheiten, aber wenn von Ihrem Lehrer nicht anders angewiesen, können Sie die Zahl auf 12,57 Einheiten aufrunden. 

Wir gebrauchen D`, nicht2r, denn dein mathematisches Problem sagt dir was D bedeutet. Es ist jedoch wichtig, diesen Schritt zu verstehen, damit Sie nicht verwirrt werden, wenn Ihr Lehrer oder Ihr Mathebuch 2r verwendet, wo Sie eine haben D würde erwarten. 
Selbst die π-Taste auf einem Taschenrechner verwendet nicht den genauen Wert von π, obwohl er sehr genau ist. 

π x d = (C / d) x d d = C 
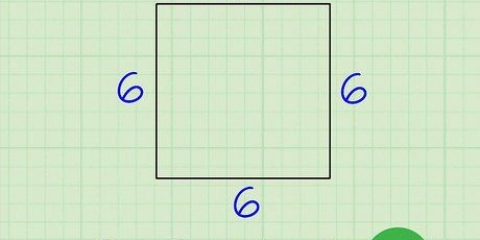
Wenn der Durchmesser beispielsweise sechs beträgt, erhalten Sie (3.14) x (6) = 18.84. Im gleichen Beispiel, aber mit der π-Taste eines Taschenrechners für mehr Genauigkeit, erhalten Sie π x 6 = 18.84956... aber wenn nicht anders angegeben, können Sie die Zahl auf 18,85 aufrunden. 


A = r A / π = πr / π = r (A/π) = √(r) = r r = √(A/π) 
C = 2πr C = 2π(√(A/π)) 
Die Antwort für dieses Beispiel ist 13.72937... aber wenn nicht anders angegeben, können Sie die Antwort auf runden 13.73. 


Stellen Sie sicher, dass Sie die Schnur mehr als einmal darum wickeln. Sie sollten am Ende eine einzelne Schlaufe haben, damit es keinen Teil des Kreises gibt, in dem das Seil doppelt gewickelt ist. 

Den umfang eines kreises ermitteln
Der Umfang eines Kreises ist der Abstand um seinen Rand. Wenn ein Kreis einen Umfang von 2 Meilen hat, müssen Sie den Kreis 2 Meilen umrunden, bevor Sie zum Ausgangspunkt zurückkehren. Wenn Sie jedoch an einem geometrischen Problem arbeiten, müssen Sie Ihren Stuhl nicht aufstehen. Lesen Sie die Aufgabe sorgfältig durch, um herauszufinden, ob der „Radius“ (r), der „Durchmesser“ (d) oder die „Fläche“ (A) des Kreises gegeben ist, und suchen Sie dann den Teil dieses Artikels, der Ihnen helfen soll mit der Aufgabe. Es gibt auch Anweisungen zum Ermitteln des Umfangs eines vorhandenen kreisförmigen Objekts, das Sie messen möchten.
Schritte
Methode 1 von 4: Bestimmung des Umfangs anhand des Radius

1. Zeichne einen `Strahl` auf den Kreis. Zeichnen Sie eine Linie vom Mittelpunkt des Kreises zu einer beliebigen Position am Rand des Kreises. Diese Linie ist der "Radius" des Kreises, der in mathematischen Gleichungen und Formeln oft als "r" geschrieben wird.
- `Anmerkung: Wenn der Radius in der mathematischen Aufgabe nicht angegeben ist, sind dies möglicherweise nicht die richtigen Anweisungen. Sehen Sie, ob die Angaben zum Durchmesser oder zur Oberfläche für die Aufgabe nützlicher sind.

2. Zeichne einen `Durchmesser` über den Kreis. Verlängern Sie die gerade gezeichnete Linie so, dass sie die Kreiskante auf der anderen Seite erreicht. Du hast gerade einen zweiten Strahl gezeichnet. Die beiden addierten Radien haben eine Länge von `2 x Radius`, geschrieben als 2r. Die Länge dieser Linie ist der "Durchmesser" des Kreises, oft geschrieben als D.

3. (`pi`) verstehen. Das Symbol π, auch geschrieben als Pi ist keine magische Zahl, die bei solchen mathematischen Aufgaben verwendet wird. Eigentlich wurde die Zahl π ursprünglich durch das Messen von Kreisen `entdeckt`: Wenn man den Umfang eines beliebigen Kreises misst (zum Beispiel mit einem Maßband) und dann durch den Durchmesser dividiert, erhält man immer die gleiche Zahl. Diese Zahl ist ungewöhnlich, da sie nicht als einfacher Bruch oder Dezimalzahl geschrieben werden kann. Stattdessen können wir es auf eine Zahl wie 3,14 aufrunden, was "gut genug" ist.

4. Schreiben Sie die Definition von π als Algebraproblem. Wie oben erklärt, bedeutet π einfach `die Zahl, die man erhält, wenn man den Umfang durch den Durchmesser teilt`. In Form einer mathematischen Formel lautet dies: = C / d. Da wir wissen, dass der Durchmesser 2 x dem Radius entspricht, können wir dies auch schreiben als = C / 2r.

5. Ändern Sie dieses Problem so, dass Sie dieses Problem für den Umfang C . lösen. Wir wollen wissen, was der Umfang ist (C in dieser mathematischen Aufgabe). Wenn Sie beide Seiten mit multiplizieren 2r du erhältst π x 2r = (C / 2r) x 2r, und das ist das gleiche wie 2πr = C.

6. Ersetzen Sie die Zahlen, um nach C . aufzulösen. Jetzt wissen wir das 2πr = C. Kehren Sie zur ursprünglichen mathematischen Aufgabe zurück, um zu sehen, was R (der Radius) ist. Ersetzen Sie dann π durch 3.14 oder verwenden Sie die π-Taste auf Ihrem Taschenrechner, um eine genauere Antwort zu erhalten. Berechnen Sie 2πr mit diesen Zahlen. Die Antwort, die Sie erhalten, ist der Umfang.
Methode 2 von 4: Umfangsbestimmung anhand des Durchmessers

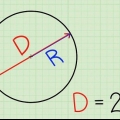
1. Verstehe was ein `Durchmesser` ist. Legen Sie Ihren Bleistift auf den Rand des Kreises. Zeichnen Sie eine Linie durch die Mitte des Kreises und die Kante auf der anderen Seite. Diese Linie (von Kante zu Kante und durch die Mitte) ist der "Durchmesser" des Kreises, oft geschrieben als D bei mathematischen Problemen.
- Die Linie geht genau durch den Mittelpunkt des Kreises, nicht irgendwo im Kreis.
- Anmerkung: Wenn die Anweisung nicht die Länge des Durchmessers angibt, verwenden Sie eine andere Methode.

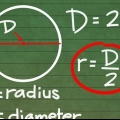
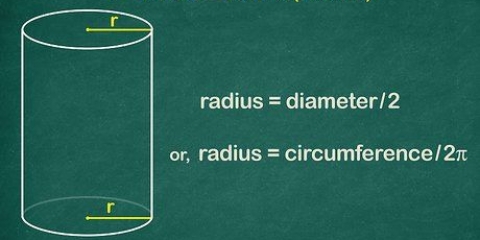
2. Erfahren Sie, was d = 2r bedeutet. Der `Radius` des Kreises, auch geschrieben als R, ist der Abstand vom Mittelpunkt zum Rand des Kreises. Da der Durchmesser von Kante zu Kante durch den Kreis geht, durch die Mitte, ist der Durchmesser gleich zwei Radien. Eine einfache Möglichkeit, dies zu schreiben, ist d = 2r. Das bedeutet, dass du D kann immer ersetzt werden durch 2r in einer mathematischen Aufgabe und umgekehrt.

3. (`pi`) verstehen. Das Symbol π, auch geschrieben als Pi ist keine magische Zahl, die bei solchen mathematischen Aufgaben verwendet wird. Eigentlich wurde die Zahl π ursprünglich durch das Messen von Kreisen `entdeckt`: Wenn man den Umfang eines beliebigen Kreises misst (zum Beispiel mit einem Maßband) und dann durch den Durchmesser dividiert, erhält man immer die gleiche Zahl. Diese Zahl ist ungewöhnlich, da sie nicht als einfacher Bruch oder Dezimalzahl geschrieben werden kann. Stattdessen können wir es auf eine Zahl wie 3,14 aufrunden, was "gut genug" ist.

4. Schreiben Sie die Definition von π als Algebraproblem. Wie oben erklärt, bedeutet π einfach `die Zahl, die man erhält, wenn man den Umfang durch den Durchmesser teilt`. In Form einer mathematischen Formel lautet dies: = Umfang / Durchmesser oder = C / d.

5. Ändern Sie dieses Problem so, dass Sie dieses Problem für den Umfang C . lösen. Wir wollen wissen, was der Umfang ist, also brauchen wir C nur auf einer Seite. Tun Sie dies, indem Sie jede Seite der Gleichung mit d multiplizieren:

6. Ersetze die Zahlen und löse nach C . auf. Kehren Sie zum ursprünglichen Problem zurück, um den Durchmesser zu sehen, und ersetzen Sie das d in dieser Gleichung durch diese Zahl. Ersetzen Sie π durch eine Rundung wie 3,14 oder verwenden Sie die π-Taste auf Ihrem Taschenrechner, um ein genaueres Ergebnis zu erhalten. Multiplizieren Sie die Werte und d miteinander und Sie erhalten den Umfang C.
Methode 3 von 4: Ermitteln des Umfangs anhand der Fläche

1. Verstehe, wie die Fläche eines Kreises berechnet wird. Normalerweise ist der Bereich (ein) eines Kreises nicht direkt gemessen. Stattdessen messen Sie den Radius (R) des Kreises und berechne dann die Fläche mit der Formel A = r. Der Grund, warum diese Formel Sinn macht, ist etwas schwer zu erklären, aber Sie können mehr erfahren über diesen Link wenn Sie interessiert und gewillt sind, einer schwereren Algebra auf den Grund zu gehen.
- Anmerkung: Wenn die mathematische Aufgabe die Fläche des Kreises nicht erwähnt, müssen Sie möglicherweise eine andere Methode als in diesem Artikel verwenden.

2. Lerne eine Formel zur Berechnung des Umfangs. Der Umfang (C) ist der Abstand um den Kreis. Das berechnest du im Allgemeinen mit der Formel C=2πr, aber weil wir noch nicht wissen wie der radius ist (R), müssen wir einige Zeit damit verbringen, den Wert von herauszufinden R bevor wir die Gleichung lösen können.

3. Verwenden Sie die Flächenformel, um r auf einer Seite zu erhalten. Da A = πr, können wir diese Formel umstellen, um stattdessen nach r aufzulösen. Wenn Sie die folgenden Schritte als schwierig empfinden, möchten Sie vielleicht zuerst einige einfachere Algebra-Aufgaben ausprobieren oder einige Techniken zum Verständnis der Algebra üben.

4. Ändere die Umfangsformel mit dem, was du gefunden hast. Jedes Mal, wenn Sie eine Gleichung haben wie r = √(A/π), Kannst du die eine Seite der Gleichung durch die andere ersetzen?. Verwenden wir diese Technik, um die obige Umfangsformel zu erhalten, C=2πr, wechseln. Für dieses Problem kennen wir den Wert von r nicht, aber den von A. Ändern wir es wie folgt, um das Problem lösbar zu machen:

5. Ersetzen Sie die Zahlen, um den Umfang zu finden. Verwenden Sie die in der Aufgabe angegebene Fläche, um den Umfang des Umfangs zu ermitteln. Wenn beispielsweise der Bereich (ein) eines Kreises ist 15 Quadrateinheiten, dann fülle aus 2π(√(15/π)) in deinen Taschenrechner. Vergiss die Klammern nicht.
Methode 4 von 4: Bestimmung des Umfangs eines echten Kreises

1. Verwenden Sie diese Methode, um echte kreisförmige Objekte zu messen. Sie können den Umfang von Kreisen messen, die Sie in der realen Welt finden, nicht nur in Problemen. Probiere es auf einem Fahrradrad, einer Pizza oder einer Münze aus.

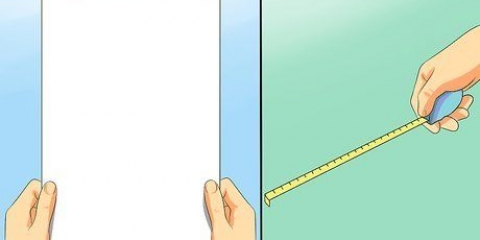
2. Nimm ein Stück Schnur und ein Lineal. Die Schnur sollte lang genug sein, um den Kreis einmal zu umwickeln, und flexibel genug, um fest zu sitzen. Du benötigst später etwas, um das Seil zu messen, z. B. ein Lineal oder ein Maßband. Die Saite lässt sich leichter messen, wenn das Lineal länger als die Saitenlänge ist.

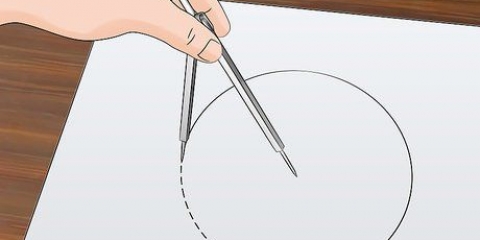
3. Wickeln Sie die Schnur einmal um den Kreis. Beginnen Sie damit, ein Ende der Schnur entlang der Kante des Kreises zu platzieren. Schlingen Sie das Seil um den Kreis und ziehen Sie es fest. Wenn Sie eine Münze oder einen anderen dünnen Gegenstand messen, können Sie die Schnur möglicherweise nicht fest daran ziehen. Legen Sie das runde Objekt flach hin und legen Sie die Schnur so eng wie möglich darum herum.

4. Markiere oder schneide die Schnur. Suchen Sie die Stelle auf der Saite, an der die Schleife endet und das Ende der Saite berührt, mit der Sie begonnen haben. Markiere diese Stelle mit einem Marker oder schneide das Seil an dieser Stelle durch.

5. Lösen Sie das Seil und messen Sie es mit einem Lineal. Nehmen Sie das umwickelte Seil und messen Sie es mit einem Lineal. Wenn Sie einen Marker verwendet haben, messen Sie nur vom Ende der Schnur bis zum Marker. Dies ist der Teil der Schnur, der sich um den Kreis wickelt, und da der Umfang eines Kreises nur die Entfernung um den Kreis ist, haben Sie die Antwort gefunden! Die Länge dieses Seils entspricht dem Umfang des Kreises.
Tipps
- Sie können den Plural von Radius als Radien oder als Radien schreiben.
"Den umfang eines kreises ermitteln"
Оцените, пожалуйста статью