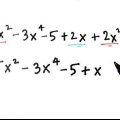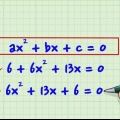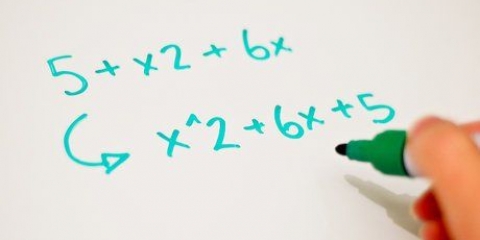Bei (x + 3x) sehen wir, dass x gleich ist. Bei (-6x - 18) sehen wir, dass -6 gleich ist. 
Durch Faktorisieren von x erhalten wir x(x + 3). Durch Zerlegen von -6 aus dem zweiten Stück erhalten wir -6(x + 3). 
Dies ergibt (x + 3)(x - 6). 
Die Lösungen sind -3 und √6. 

Faktoren sind die Zahlen, die du miteinander multiplizieren kannst, um eine andere Zahl zu erhalten. In diesem Fall sind dies die Faktoren von 10, oder "D": 1, 2, 5 und 10. 
Beginnen Sie mit dem ersten Faktor,1. Ersatz "1" für jede "x" im vergleich:
(1) - 4(1) - 7(1) + 10 = 0 Dies ergibt: 1 - 4 - 7 + 10 = 0. Da 0 = 0 eine wahre Aussage ist, wissen Sie, dass x = 1 die Lösung ist. 
"x = 1" ist das gleiche wie "x - 1 = 0" oder "(x - 1)". Du hast nur einen "1" von jeder Seite der Gleichung abgezogen. 
Kannst du (x - 1) von x . faktorisieren? Nein das ist nicht möglich. Aber wenn Sie zuerst a -x von der zweiten Variablen borgen: x(x - 1) = x - x. Können Sie (x - 1) aus dem, was von der zweiten Variablen übrig bleibt, faktorisieren?? Nein, das ist hier auch nicht möglich. Sie müssen sich wieder etwas von der dritten Variable leihen, die 3x von -7x . ist. Dies gibt uns -3x(x - 1) = -3x + 3x. Da Sie 3x von -7x genommen haben, ist die dritte Variable jetzt -10x und die Konstante ist 10. Kannst du das auflösen. Ja, sicher! -10(x - 1) = -10x + 10. Was Sie getan haben, ist die Variablen neu anzuordnen, damit Sie den Faktor (x - 1) aus der gesamten Gleichung erhalten können. Die modifizierte Gleichung sieht so aus: x - x - 3x + 3x - 10x + 10 = 0, ist aber immer noch dieselbe wie x - 4x - 7x + 10 = 0. 
x(x - 1) - 3x(x - 1) - 10(x - 1) = 0. Sie können diese neu anordnen, um das Auflösen zu erleichtern: (x - 1)(x - 3x - 10) = 0. Hier versuchen Sie nur zu faktorisieren (x - 3x - 10). Die Faktoren werden dann zu (x + 2)(x - 5). 
(x - 1)(x + 2)(x - 5) = 0 Dies ergibt die Lösungen für 1, -2 und 5. Setze -2 in die Gleichung ein: (-2) - 4(-2) - 7(-2) + 10 = -8 - 16 + 14 + 10 = 0. Setze 5 in die Gleichung ein: (5) - 4(5) - 7(5) + 10 = 125 - 100 - 35 + 10 = 0.
Faktorisieren eines polynoms dritten grades
In diesem Artikel geht es um das Faktorisieren eines kubischen Polynoms, auch Polynom genannt. Wir werden untersuchen, wie wir dies mithilfe der Gruppierung und der Faktoren des freien Termes erreichen können.
Schritte
Teil1 von 2: Auflösen durch Gruppieren

1. Teile das Polynom in zwei Gruppen. Das Dividieren des Polynoms hilft bei der Lösung jedes einzelnen Teils.
- Angenommen, wir arbeiten mit dem folgenden Polynom:" x + 3x - 6x - 18 = 0. Unterteilen wir dies in (x + 3x) und (-6x - 18)

2. Versuchen Sie herauszufinden, was in jeder Gruppe gleich ist.

3. Entfernen Sie diese gleichen Faktoren aus den beiden Termen.

4. Wenn jeder der beiden Terme den gleichen Faktor enthält, können Sie diese Faktoren kombinieren.

5. Finden Sie die Lösung, indem Sie auf die Wurzeln schauen. Wenn Sie x in einer Quadratwurzel haben, denken Sie daran, dass sowohl positive als auch negative Zahlen für diese Gleichung gültig sind.
Teil 2 von 2: Factoring mit der kostenlosen Laufzeit

1. Ordnen Sie den Ausdruck in der folgenden Form neu an: ax+bx+cx+d.
- Angenommen, Sie arbeiten mit der Gleichung: x - 4x - 7x + 10 = 0.

2. Finden Sie alle Faktoren von "D". Die Konstante "D" wird die Zahl ohne Variablen daneben wie "x".

3. Finden Sie einen Faktor, der das Polynom gleich Null macht. Wir wollen bestimmen, welcher Faktor das Polynom gleich Null macht, wenn wir diesen Faktor anwenden für "x" fülle die Gleichung aus.
(1) - 4(1) - 7(1) + 10 = 0

4. Jetzt geh alles neu anordnen. Wenn x=1 dann ist es möglich, diese Gleichung etwas anders zu schreiben, ohne die Bedeutung zu ändern.

5. Ziehe die Quadratwurzel der Gleichung heraus. "(x - 1)" ist die Wurzel. Versuchen Sie, diese aus dem Rest der Gleichung herauszurechnen. Tun Sie dies mit jeweils einem Polynom.

6. Fahren Sie mit dem Ersetzen der Faktoren der freien Laufzeit fort. Sehen Sie sich die Zahlen an, die Sie in Schritt 5 mit (x - 1) gelöst haben:

7. Ihre Lösung sind die faktorisierten Wurzeln. Überprüfen Sie diese Lösung, indem Sie jede von ihnen wieder in die ursprüngliche Gleichung einsetzen.
Tipps
- Die kubische Gleichung ist das Produkt von 3 Gleichungen ersten Grades oder einer Gleichung ersten Grades und einer nicht faktorisierbaren Gleichung zweiten Grades. Im letzteren Fall verwenden Sie nach dem Finden des Polynoms ersten Grades eine lange Division, um das Polynom zweiten Grades zu finden.
- Es gibt keine kubischen Polynome, die bei reellen Zahlen nicht faktorisiert werden können, da diese Gleichung eine Quadratwurzel aus reellen Zahlen haben muss. Gleichungen dritten Grades wie x + x + 1, die eine irrationale reelle Wurzel haben, können nicht in Polynome mit ganzen oder rationalen Zahlen als Koeffizienten eingerechnet werden. Obwohl es in die Gleichung selbst eingerechnet werden kann, kann es nicht auf ein ganzzahliges Polynom reduziert werden.
Methode 2 bedeutet lange Division zweier Polynome, a.v:
(x-1) ∕x³ - 4x²-7x+10 ∕
- x³ - 1x².................................= (x-1) (x²)
- - 3x²-7x
- 3x²+ 3x.........................= (x-1) (-3x)
- - 10x + 10
- 10x + 10................= (x-1) (-10)
- 0............................ x²- 3x-10 (Quotient)
Die Bestimmungen x², -3x und -10 des Quotienten erhält man, indem man immer den 1. Term des Divisors ( x ) vom ersten Term des Dividenden subtrahiert, bzw. was davon übrig ist ( x³, -3x², -10x ).
"Faktorisieren eines polynoms dritten grades"
Оцените, пожалуйста статью