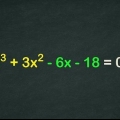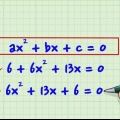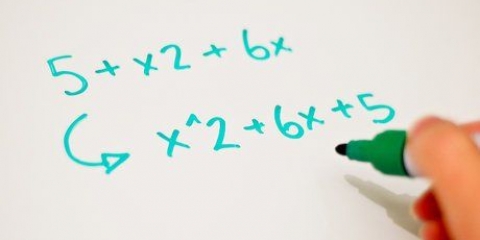→
→ 
 →
→ 
 →
→ 
Beachten Sie, wie die Minuszeichen vor der 2 bleiben. Wenn ein Term subtrahiert wird, bleibt das Minuszeichen davor. 
Übungsaufgabe: .
. Faktoren von 3:1, 3 Faktoren von 6: 1, 2, 3, 6. `Der größte gemeinsame Teiler ist 3`. 
Übungsaufgabe: .
. Finden Sie die größten gemeinsamen Teiler: 3 Um Faktor aus beiden Termen zu entfernen:

Übungsaufgabe:
Finden Sie die größten gemeinsamen Teiler: 3 Um Faktor aus beiden Termen zu entfernen:
Faktor mit neuem Ausdruck multiplizieren:
Endgültige gelöste Antwort: 

So ordnen Sie Bedingungen neu an:
Den größten gemeinsamen Teiler finden:
Um Faktor aus beiden Termen zu entfernen:
Faktor mit neuem Ausdruck multiplizieren:
Prüfe die Antwort:


Übungsaufgabe:
Gleich Null:


Übungsaufgabe:
Gleich Null:
Sich auflösen:

Übungsaufgabe:
Gleich Null:
Sich auflösen:
Machen Sie beide Terme gleich Null 0: 




y = 0 

y = 4 


 Diese Antwort ist richtig
Diese Antwort ist richtig

 Diese Antwort ist auch richtig.
Diese Antwort ist auch richtig.

Ursprünglicher Auftrag:
So ordnen Sie Bedingungen neu an:
So führen Sie ähnliche Begriffe zusammen:
Finden Sie die größten gemeinsamen Teiler:
Sich auflösen:

Die Formel für die Differenz perfekter Quadrate:
Übungsaufgabe:
Bestimme die Quadratwurzeln: 

Wende Quadratwurzeln auf die Formel an: 

Formel für die Differenz der dritten Potenzen:
Übungsaufgabe:
Bestimme die Kubikwurzeln: ![Faktorisieren von Binomialen {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorisieren von Binomialen {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Wende Würfel auf die Formel an: 

Formel für die Summe perfekter Würfel:
Übungsaufgabe:
Bestimme die Kubikwurzeln: ![Faktorisieren von Binomialen {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorisieren von Binomialen {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)
Wende die Würfel auf die Formel an: 
Faktorisieren von binomialen
In der Algebra sind Binomiale Ausdrücke mit zwei Begriffen, die durch ein Plus- oder Minuszeichen verbunden sind, wie z 
Schritte
Teil 1 von 3: Binomialzahlen faktorisieren

1. Wiederholen Sie die Grundlagen des Factorings noch einmal. Factoring teilt eine große Zahl in ihre einfachsten Teiler. Jeder dieser Teile wird als „Faktor“ bezeichnet. Zum Beispiel ist die Zahl 6 durch vier verschiedene Zahlen teilbar: 1, 2, 3 und 6. 1, 2, 3 und 6 sind also die Faktoren von 6.
- Die Faktoren von 32 sind 1, 2, 4, 8, 16 und 32
- Sowohl die `1` als auch die Zahl, die Sie faktorisieren, sind immer Faktoren. Die Faktoren einer kleinen Zahl wie 3 sind also nur 1 und 3.
- Faktoren sind nur die Zahlen, die vollständig teilbar sind, also die `ganzen` Zahlen. Sie könnten 32 durch 3,564 oder 21,4952 teilen, aber das sind keine Faktoren, sondern nur Dezimalzahlen.

2. Listen Sie die Begriffe des Binomials auf, um sie leichter lesbar zu machen. Ein Binomial ist nichts anderes als die Addition oder Subtraktion von zwei Termen, von denen mindestens einer eine Variable enthält. Manchmal haben diese Variablen Exponenten, wie z  oder
oder  . Wenn Sie zum ersten Mal versuchen, Binomie zu faktorisieren, hilft es, die Gleichungen in absteigenden Variablenwerten zu ordnen, was bedeutet, dass der größte Exponent zuletzt kommt. Zum Beispiel:
. Wenn Sie zum ersten Mal versuchen, Binomie zu faktorisieren, hilft es, die Gleichungen in absteigenden Variablenwerten zu ordnen, was bedeutet, dass der größte Exponent zuletzt kommt. Zum Beispiel:
 oder
oder  . Wenn Sie zum ersten Mal versuchen, Binomie zu faktorisieren, hilft es, die Gleichungen in absteigenden Variablenwerten zu ordnen, was bedeutet, dass der größte Exponent zuletzt kommt. Zum Beispiel:
. Wenn Sie zum ersten Mal versuchen, Binomie zu faktorisieren, hilft es, die Gleichungen in absteigenden Variablenwerten zu ordnen, was bedeutet, dass der größte Exponent zuletzt kommt. Zum Beispiel: →
→ 
 →
→ 
 →
→ 

3. Finden Sie den größten gemeinsamen Teiler beider Terme. Dies bedeutet, dass Sie nach der größten Zahl suchen, durch die beide Teile des Binomials teilbar sind. Wenn dies nicht funktioniert, faktoriere beide Zahlen einzeln und schau, was die höchste übereinstimmende Zahl ist. Zum Beispiel:
 .
.
4. Teilen Sie den größten gemeinsamen Teiler für jeden Begriff. Wenn Sie den gemeinsamen Nenner kennen, müssen Sie ihn aus jedem Begriff entfernen. Beachten Sie, dass Sie die Terme nur dividieren, wodurch jeder ein kleineres Divisionsproblem wird. Bei richtiger Ausführung haben beide Gleichungen den gleichen Faktor:
 .
.

5. Multiplizieren Sie Ihren Faktor mit dem resultierenden Ausdruck, um abzurunden. Im letzten Problem hast du eine 3 entfernt und du bekommst  . Aber Sie wollen die 3 nicht komplett loswerden, sondern einfach einkalkulieren, um die Dinge zu vereinfachen. Sie können nicht einfach Zahlen löschen, ohne sie zurückzusetzen! Multiplizieren Sie den Faktor mit dem Ausdruck, um diesen Abschnitt zu vervollständigen. Zum Beispiel:
. Aber Sie wollen die 3 nicht komplett loswerden, sondern einfach einkalkulieren, um die Dinge zu vereinfachen. Sie können nicht einfach Zahlen löschen, ohne sie zurückzusetzen! Multiplizieren Sie den Faktor mit dem Ausdruck, um diesen Abschnitt zu vervollständigen. Zum Beispiel:
 . Aber Sie wollen die 3 nicht komplett loswerden, sondern einfach einkalkulieren, um die Dinge zu vereinfachen. Sie können nicht einfach Zahlen löschen, ohne sie zurückzusetzen! Multiplizieren Sie den Faktor mit dem Ausdruck, um diesen Abschnitt zu vervollständigen. Zum Beispiel:
. Aber Sie wollen die 3 nicht komplett loswerden, sondern einfach einkalkulieren, um die Dinge zu vereinfachen. Sie können nicht einfach Zahlen löschen, ohne sie zurückzusetzen! Multiplizieren Sie den Faktor mit dem Ausdruck, um diesen Abschnitt zu vervollständigen. Zum Beispiel:




6. Überprüfen Sie Ihre Arbeit, indem Sie mit der ursprünglichen Gleichung multiplizieren. Wenn Sie alles richtig gemacht haben, können Sie leicht überprüfen, ob Sie es richtig gemacht haben. Multiplizieren Sie Ihren Faktor mit den beiden einzelnen Begriffen in Klammern. Wenn es mit dem ursprünglichen Binomial übereinstimmt, haben Sie alles richtig gemacht. Von Anfang bis Ende lösen wir den Ausdruck  weiter zum Üben:
weiter zum Üben:
 weiter zum Üben:
weiter zum Üben:




Teil 2 von 3: Binomiale faktorisieren, um Gleichungen zu lösen

1. Faktor zur Vereinfachung von Gleichungen, damit sie leichter zu lösen sind. Beim Lösen einer Gleichung mit Binomialen, insbesondere komplexen Binomialen, kann es so aussehen, als ob es keine Möglichkeit gibt, alles in Einklang zu bringen. Versuchen Sie beispielsweise Folgendes zu lösen:  . Eine Möglichkeit, dies insbesondere bei Exponenten zu tun, besteht darin, zuerst zu faktorisieren.
. Eine Möglichkeit, dies insbesondere bei Exponenten zu tun, besteht darin, zuerst zu faktorisieren.
 . Eine Möglichkeit, dies insbesondere bei Exponenten zu tun, besteht darin, zuerst zu faktorisieren.
. Eine Möglichkeit, dies insbesondere bei Exponenten zu tun, besteht darin, zuerst zu faktorisieren. - Übungsaufgabe:
- Denken Sie daran, dass Binome nur zwei Terme haben können. Wenn es mehr als zwei Begriffe gibt, müssen Sie lernen Polynome zu lösen.

2. Addiere und subtrahiere, sodass eine Seite der Gleichung gleich Null ist. Diese ganze Strategie beruht auf einer der grundlegendsten Tatsachen der Mathematik: Etwas, das mit Null multipliziert wird, muss gleich Null sein. Wenn Ihre Gleichung also gleich Null ist, muss einer der faktorisierten Terme gleich Null sein! Zu Beginn addieren und subtrahieren Sie so, dass eine Seite gleich Null ist.




3. Lösen Sie die Nicht-Null-Seite wie gewohnt auf. An diesem Punkt tust du nur so, als ob die andere Seite nicht existiert. Finden Sie den größten gemeinsamen Teiler, teilen Sie ihn und erstellen Sie dann Ihren faktorisierten Ausdruck.




4. Setzen Sie die Terme innerhalb und außerhalb der Klammern gleich Null. In der Übungsaufgabe multiplizieren Sie 2y mit (4 – y), und diese muss gleich Null sein. Da etwas mit Null multipliziert gleich Null ist, bedeutet dies, dass 2y oder (4 – y) gleich Null sein muss. Stellen Sie zwei separate Gleichungen auf, um herauszufinden, welchen Wert y haben muss, um eine Seite gleich Null zu machen.






5. Löse beide Gleichungen nach Null für die endgültige Antwort oder Antworten. Sie können eine oder mehrere Antworten erhalten. Denken Sie daran, dass nur eine Seite gleich Null sein muss, damit Sie ein paar verschiedene Werte für y erhalten, die dieselbe Gleichung lösen. Die letzten Schritte der Übungsaufgabe:





6. Wende deine Antworten wieder auf die ursprüngliche Gleichung an, um sicherzustellen, dass sie richtig sind. Sobald Sie die richtigen Werte für y gefunden haben, sollten Sie diese verwenden können, um die Gleichung zu lösen. Dies ist so einfach wie das Ausprobieren jedes Wertes von y anstelle der Variablen wie unten gezeigt. Die Antworten sind y = 0 und y = 4, also:


 Diese Antwort ist richtig
Diese Antwort ist richtig

 Diese Antwort ist auch richtig.
Diese Antwort ist auch richtig.Teil3 von 3: Umgang mit härteren Problemen

1. Denken Sie daran, dass Variablen auch mit Exponenten als Faktoren gelten. Denken Sie daran, dass es beim Faktorisieren darum geht, zu bestimmen, welche Zahlen in die ganze Zahl passen. Der Ausdruck  ist eine andere Art zu sagen
ist eine andere Art zu sagen  . Dies bedeutet, dass Sie jedes x außerhalb von Klammern setzen können, wenn der andere Begriff auch eine hat. Behandeln Sie Variablen wie reguläre Zahlen. Zum Beispiel:
. Dies bedeutet, dass Sie jedes x außerhalb von Klammern setzen können, wenn der andere Begriff auch eine hat. Behandeln Sie Variablen wie reguläre Zahlen. Zum Beispiel:
 ist eine andere Art zu sagen
ist eine andere Art zu sagen  . Dies bedeutet, dass Sie jedes x außerhalb von Klammern setzen können, wenn der andere Begriff auch eine hat. Behandeln Sie Variablen wie reguläre Zahlen. Zum Beispiel:
. Dies bedeutet, dass Sie jedes x außerhalb von Klammern setzen können, wenn der andere Begriff auch eine hat. Behandeln Sie Variablen wie reguläre Zahlen. Zum Beispiel: kann faktorisiert werden, da beide Terme ein t . enthalten. Die endgültige Antwort wird sein
- Sie können sogar mehrere Variablen gleichzeitig außerhalb von Klammern platzieren. Zum Beispiel in
beide Begriffe enthalten dasselbe
. Du kannst das auflösen in

2. Erkenne noch nicht vereinfachte Binome, indem du gleiche Terme kombinierst. Nehmen Sie zum Beispiel den Ausdruck  . Hier sieht es so aus, als hätte man es mit vier Begriffen zu tun, doch bei genauerem Hinsehen stellt man fest, dass es nur zwei sind. Sie können ähnliche Begriffe hinzufügen und da sowohl 6 als auch 14 keine Variable haben und 2x und 3x dieselbe Variable teilen, können sie zusammengeführt werden. Das Auflösen ist dann einfach:
. Hier sieht es so aus, als hätte man es mit vier Begriffen zu tun, doch bei genauerem Hinsehen stellt man fest, dass es nur zwei sind. Sie können ähnliche Begriffe hinzufügen und da sowohl 6 als auch 14 keine Variable haben und 2x und 3x dieselbe Variable teilen, können sie zusammengeführt werden. Das Auflösen ist dann einfach:
 . Hier sieht es so aus, als hätte man es mit vier Begriffen zu tun, doch bei genauerem Hinsehen stellt man fest, dass es nur zwei sind. Sie können ähnliche Begriffe hinzufügen und da sowohl 6 als auch 14 keine Variable haben und 2x und 3x dieselbe Variable teilen, können sie zusammengeführt werden. Das Auflösen ist dann einfach:
. Hier sieht es so aus, als hätte man es mit vier Begriffen zu tun, doch bei genauerem Hinsehen stellt man fest, dass es nur zwei sind. Sie können ähnliche Begriffe hinzufügen und da sowohl 6 als auch 14 keine Variable haben und 2x und 3x dieselbe Variable teilen, können sie zusammengeführt werden. Das Auflösen ist dann einfach:





3. Erkenne die besondere `Differenz der perfekten Quadrate`. Ein perfektes Quadrat ist eine Zahl, deren Wurzel eine ganze Zahl ist, wie z 
 ,
, 
 , oder auch
, oder auch 
 Wenn Ihr Binomial eine Minussumme mit zwei perfekten Quadraten ist, wie z
Wenn Ihr Binomial eine Minussumme mit zwei perfekten Quadraten ist, wie z  , Dann kannst du sie einfach in dieser Formel verwenden:
, Dann kannst du sie einfach in dieser Formel verwenden:

 ,
, 
 , oder auch
, oder auch 
 Wenn Ihr Binomial eine Minussumme mit zwei perfekten Quadraten ist, wie z
Wenn Ihr Binomial eine Minussumme mit zwei perfekten Quadraten ist, wie z  , Dann kannst du sie einfach in dieser Formel verwenden:
, Dann kannst du sie einfach in dieser Formel verwenden:





4. Lernen Sie, den `Unterschied der perfekten Würfel` zu vereinfachen. Wie die perfekten Quadrate ist dies eine einfache Formel, bei der zwei Würfel voneinander subtrahiert werden. Zum Beispiel,  . Finden Sie wie zuvor die Kubikwurzel von jedem und verwenden Sie diese in der Formel:
. Finden Sie wie zuvor die Kubikwurzel von jedem und verwenden Sie diese in der Formel:
 . Finden Sie wie zuvor die Kubikwurzel von jedem und verwenden Sie diese in der Formel:
. Finden Sie wie zuvor die Kubikwurzel von jedem und verwenden Sie diese in der Formel:

![Faktorisieren von Binomialen {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorisieren von Binomialen {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)


5. Wisse, dass die Summe perfekter Würfel auch in eine Formel passt. Im Gegensatz zum Unterschied der perfekten Quadrate können Sie hinzugefügte Würfel verwenden, wie z  , auch leicht zu finden mit einer einfachen Formel. Dies ist fast genau das gleiche wie oben, aber mit einigen Vor- und Nachteilen vertauscht. Die Formel ist genauso einfach wie die anderen beiden, und Sie müssen nur die beiden Würfel in der Aufgabe erkennen:
, auch leicht zu finden mit einer einfachen Formel. Dies ist fast genau das gleiche wie oben, aber mit einigen Vor- und Nachteilen vertauscht. Die Formel ist genauso einfach wie die anderen beiden, und Sie müssen nur die beiden Würfel in der Aufgabe erkennen:
 , auch leicht zu finden mit einer einfachen Formel. Dies ist fast genau das gleiche wie oben, aber mit einigen Vor- und Nachteilen vertauscht. Die Formel ist genauso einfach wie die anderen beiden, und Sie müssen nur die beiden Würfel in der Aufgabe erkennen:
, auch leicht zu finden mit einer einfachen Formel. Dies ist fast genau das gleiche wie oben, aber mit einigen Vor- und Nachteilen vertauscht. Die Formel ist genauso einfach wie die anderen beiden, und Sie müssen nur die beiden Würfel in der Aufgabe erkennen:

![Faktorisieren von Binomialen {sqrt[ {3}]{8x^{3}}}=2x](https://wikimedia.org/api/rest_v1/media/math/render/svg/77ed49f7f0ab2dfb9de3438ac123641fb683a0a0)
![Faktorisieren von Binomialen {sqrt[ {3}]{27}}=3](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca5392df17ff31f62e3cae649d51dd36bde856ce)

Tipps
- Nicht alle Binome haben gemeinsame Teiler! Einige wurden bereits so weit wie möglich vereinfacht.
- Wenn Sie sich nicht sicher sind, ob es einen gemeinsamen Teiler gibt, dividieren Sie zuerst durch kleinere Zahlen. Wenn Sie beispielsweise nicht sofort sehen, dass 16 der gemeinsame Teiler von 32 und 16 ist, beginnen Sie, beide Zahlen durch 2 zu teilen. Es bleiben 16 und 8, die auch durch 8 geteilt werden können. Jetzt hast du 2 und 1, die kleinsten Faktoren. Es gibt eindeutig einen gemeinsamen Teiler größer als 8 und 2.
- Beachten Sie, dass eine sechste Potenz (x) sowohl ein perfektes Quadrat ist und ist ein perfekter Würfel. Sie können also eine der obigen Sonderformeln in beliebiger Reihenfolge auf ein Binomial anwenden, das die Differenz der perfekten sechsten Potenzen ist, z. B. x - 64. Möglicherweise finden Sie es jedoch einfacher, zuerst die Differenzformel für perfekte Quadrate anzuwenden, damit Sie das Binomial weiter faktorisieren können.
Warnungen
- Ein Binomial, das die Summe perfekter Quadrate ist, kann nicht faktorisiert werden.
"Faktorisieren von binomialen"
Оцените, пожалуйста статью