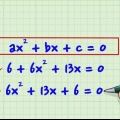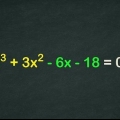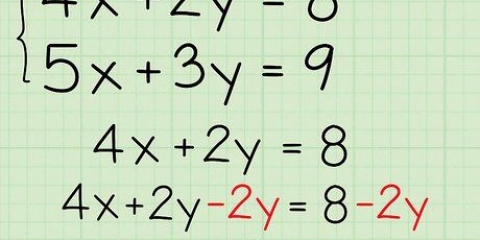Faktorisieren

Schritte
Tipps
Warnungen
Notwendigkeiten

In der Algebra ist eine quadratische Gleichung ein Polynom bestehend aus 3 Termen der Form ax + bx + c. Polynome haben viele Anwendungen in Mathematik und Naturwissenschaften, und das Lösen quadratischer Gleichungen ist eine wichtige Fähigkeit. Während die meisten quadratischen Gleichungen einfach faktorisiert werden können, gibt es mehrere Fälle, in denen eine quadratische Gleichung auf besondere Weise faktorisiert werden muss.Wenn keine der Methoden in der folgenden Anleitung nützlich ist, müssen möglicherweise Methoden zum Faktorisieren höherer Polynome verwendet werden.

Schritte

Methode 1 von 4: Division Zwei

1. Ordne die Argumente der quadratischen Gleichung vom größten zum kleinsten. Ein Argument ist eine Variable im Polynom; die normale Reihenfolge beim Platzieren der Terme ist von der höchsten Potenz zur niedrigsten. 5 + x + 6x müssen also als x + 6x + 5 . bestellt werden.

2. Schließen Sie jeden Faktor aus, der in allen drei Begriffen vorkommt. Wenn die Konstanten der quadratischen Gleichung alle Vielfache derselben Zahl sind, können Sie sie außerhalb von Klammern setzen, oder wenn jede Komponente der quadratischen Gleichung eine gleiche Variable hat, kann diese Variable außerhalb der Klammern platziert werden.

In der quadratischen Gleichung -8a + 24a + 144 ist beispielsweise jede Konstante ein Vielfaches von 8, also kann 8 außerhalb von Klammern gesetzt werden, was -8(a - 3a - 18) ergibt. Obwohl der Koeffizient -3 und die Konstante -18 beide durch -3 teilbar sind, ist der Koeffizient 1 des ersten Termes nicht weiter faktorisieren.

In der quadratischen Gleichung - x - 2x - 1 ist jeder Term durch -1 teilbar, was nach der Faktorisierung als (-1)(x + 2x + 1) geschrieben werden kann.

3. Suchen Sie nach Mustern, die das Lösen einer quadratischen Gleichung erleichtern. Für immer detailliertere Informationen und Beispiele siehe die Methode zum Lösen von Sonderfällen einer quadratischen Gleichung.

4. Versuchen Sie, wenn möglich, die quadratische Gleichung in 2 zwei Terme der Form (mx + n) (qx + r) zu teilen. Dies ist oft nur das Ausprobieren dessen, was funktioniert, aber es gibt Tricks, die dies einfacher machen. Nehmen wir zunächst an, dass der erste Term in der quadratischen Gleichung (der x-Term) gleich 1 ist (der Term sieht eher aus wie x als z.B., 3x). Die m- und q-Werte der beiden Terme sind 1, also sieht Ihre Lösung wie folgt aus (x + b) (x + d). Finden Sie dann für Ihre Gleichung der Form ax + bx + c die Werte n und r so, dass: n * r = c und n + r = b.

Im Beispiel x + 6x + 5, 5 * 1 = 5 und 5 + 1 = 6. Die Lösung ist also (x + 1)(x + 5).

Wenn nicht alle Terme in der quadratischen Gleichung positiv sind, vergessen Sie nicht, die negativen Zahlen zu berücksichtigen. Zum Beispiel x - 3x - 18 Faktor in (x - 6)(x + 3) weil -6 + 3 = -3 und -6 * 3 = -18.

5. Wenn die Konstante im ersten Term ungleich 1 ist (z.B. sieht es eher nach 3x als nach x aus), wird das Factoring etwas schwieriger und über ax + bx + c erhält man schließlich eine Lösung in der Form (mx + n)(qx + r). Für eine korrekte Lösung gilt m * q = a, m * r + n * q = b und n * r = c.

Erstellen Sie zunächst eine Liste aller möglichen Faktoren von a und c. Überprüfen Sie dann, welches Faktorenpaar funktioniert, indem Sie die oben angegebenen Einschränkungen verwenden.

Nehmen Sie zum Beispiel 3x + 10x + 8. Mögliche Faktorpaare von 3 sind 1 * 3. Mögliche Faktorpaare von 8 sind 1 * 8 und 2 * 4. Da 3 * 1 = 3 (der Term der quadratischen Gleichung), 1 * 4 + 2 * 3 = 10 (der b-Term) und 2 * 4 = 8 (der c-Term) ist, lautet die Lösung (3x + 4) ( x + 2).

Methode 2 von 4: Berücksichtigung von Sonderfällen

1. Prüfen Sie, ob die Konstante im ersten Term oder im dritten Term der Gleichung eine Primzahl ist. Eine Primzahl ist nur durch sich selbst und 1 . teilbar. Dies verringert die Anzahl möglicher Binomialfaktoren. Im vorherigen Beispiel: x + 6x + 5 gibt es nur 1 mögliche Menge von Binomialfaktoren (x + 5)(x + 1), weil 5 eine Primzahl ist.

2. Überprüfe, ob die quadratische Gleichung ein perfektes Quadrat ist. Dies erfordert, dass die Werte der Koeffizienten a und c der Gleichung ax + bx + c perfekte Quadrate sind (und positiv!), und dass der Wert von b doppelt so groß ist wie der Wert des Produkts der Quadratwurzel von a und c.

(x + a) wird zu x + 2ax + a. Zum Beispiel (x + 3) = x + 6x + 9 und (3x + 2) = 9x + 12x + 4.

Ebenso wird (x - a) zu x - 2ax + a. Zum Beispiel (x - 3) = x - 6x + 9.

3. Für einige quadratische Gleichungen der Form x - n:

(x + a)(x - a) wird zu x - a. Also kann x - 9 schnell in (x + 3) (x - 3) eingerechnet werden, und 4x - 4 = (2x + 2) (2x - 2).

Methode 3 von 4: Verwenden der abc-Formel

Für schwer oder gar nicht lösbare quadratische Gleichungen der Form ax + bx + c verwenden Sie die abc-Formel.

1. Lernen Sie, die ABC-Formel zu verwenden.

2. Geben Sie a, b und c ein und lösen Sie den ersten Teil der Formel. Angenommen, wir haben die quadratische Gleichung x + 5x + 6.

Beginnen Sie mit b - 4ac, das ist 5 - 4(1)(6) = 1. Die Quadratwurzel von 1 ist 1.

Beenden Sie, indem Sie die Gleichung lösen. -b + 1 = -5 + 1 = -4. Teilen Sie dies durch 2a (2 * 1 = 2), um -2 als Antwort zu erhalten.

3. Löse den anderen Teil. Wir wissen bereits, dass die Quadratwurzel von b - 4ac = 1. -b - 1 = -6. Teilen Sie dies durch 2a (2), um -3 . zu erhalten.

4. Überprüfen Sie Ihre Lösungen, indem Sie sie für x . ausfüllen. Manchmal sind eine oder mehrere der Antworten keine gültigen Lösungen (z. B. wenn es sich um imaginäre Zahlen handelt). Aber wenn eine quadratische Gleichung eine Lösung hat, dann wird die Gleichung sie finden.

Beachten Sie, dass wir, wenn wir diese Gleichung faktorisiert hätten, anstatt die abc-Formel zu verwenden, als Antwort (x + 2) (x + 3). Wenn Sie diese Gleichung gleich 0 setzen, erhalten Sie zwei Lösungen, x = 2 und x = -3, die wir auch mit der Formel gefunden haben.

Methode 4 von 4: Das versteckte Quadrat in einem Polynom

Einige quadratische Gleichungen sind von höherer Ordnung, aber im Wesentlichen nur quadratisch. Sobald sie als solche erkannt wurden, können Sie sie als solche behandeln, indem Sie Substitution verwenden.

1. Schauen Sie sich die Variablen in jedem Begriff an.Zum Beispiel scheint x - 7x + 12 eine Potenz von 6 zu sein, aber nach Substitution von u=x wird dies zu u - 7u + 12. Dadurch erhalten Sie eine Gleichung, die viel einfacher zu lösen ist.

Komplexere Substitutionen können helfen, kniffligere Probleme zu lösen. Zum Beispiel wird xy - 7xy + 12y zu xy(u - 7u + 12) vereinfacht und nach der Substitution u = x/y. Eine solche Ersetzung ist immer dann möglich, wenn die Summe der Potenzen der beiden Terme das Doppelte der Potenz des verbleibenden Termes ist.

2. Wenn eine solche Substitution stattfinden kann, dann ziehe das einfache Polynom heraus, in diesem Fall u - 7u + 12 = (u-3)(u-4)

3. Mache die Substitution rückgängig und wende x auf die Lösung an. Also ersetze u durch x , x - 7x + 12 = (x - 3)(x - 4). Wenn möglich oder gewünscht, kann jeder Faktor noch weiter vereinfacht werden.

Tipps

Verwenden Sie das Eisenstein-Kriterium, um schnell zu bestimmen, ob ein Polynom nicht reduzierbar und nicht faktorierbar ist. Dieses Kriterium gilt für jedes Polynom, insbesondere aber für eine quadratische Gleichung. Wenn es eine Primzahl p gibt, die die letzten beiden Terme teilbar macht und die folgenden Bedingungen erfüllt, kann das Polynom nicht reduziert werden:

Der konstante Term (das c in einer quadratischen Gleichung der Form ax + bx + c) ist ein Plural von p, aber nicht von p.
Der erste Term (hier a) ist kein Plural von p.
Zum Beispiel ist 14x + 45x + 51 irreduzibel, weil es eine Primzahl (3) hat, die sowohl 45 als auch 51 teilbar macht, aber nicht 14 und 51, die nicht durch 3 . teilbar sind.

Sie können Polynome mehrerer Variablen mit den obigen Methoden faktorisieren, wenn es sich um quadratische Gleichungen unter der Annahme einer Variablen handelt. Nehmen Sie zum Beispiel 4xy - 5x + 15y. Dies kann umgeschrieben werden als (4x)y + 15y - 5x. Beachten Sie, dass dies der Form ax + bx + c entspricht, wobei a = 4x und c = 5x. Diese Gleichung kann dann mit der abc-Formel gelöst werden.

Sie können die Faktorisierung quadratischer Gleichungen üben, indem Sie Aufgaben in einem Buch über Algebra lösen.

Warnungen

Obwohl für Quadrate wahr, quadratische Gleichungen, die faktorisiert werden können, sind nicht notwendigerweise das Produkt zweier Binärwerte. Ein Gegenbeispiel ist x + 105x + 46 = (x + 5x + 2)(x - 5x + 23).