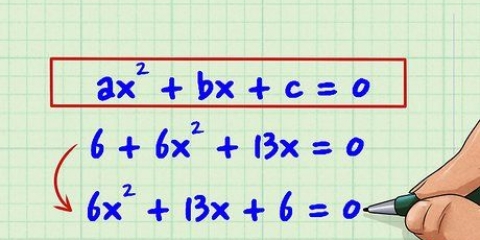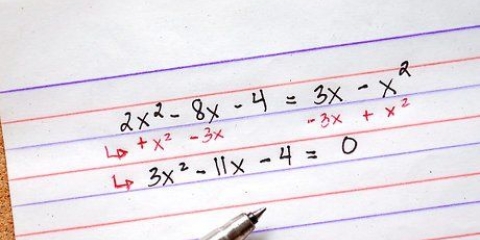Zum Beispiel kann die Variable 12y als das Produkt der Faktoren von 12 und y . umgeschrieben werden. Wir können 12y als 3(4y), 2(6y) usw. schreiben., Verwenden Sie die Faktoren von 12, die am bequemsten sind. Wir können sogar bis zu 12 Jahre gehen mehrmals sich auflösen. Mit anderen Worten, wir müssen nicht bei 3(4y) oder 2(6y) aufhören - wir können 4y und 6y in 3(2(2y) bzw. 2(3(2y)) einrechnen. Anscheinend sind diese beiden Ausdrücke äquivalent zueinander. 
Versuchen wir es mit einem Beispielproblem. Um die Gleichung 12x + 6 zu faktorisieren, suchen wir zuerst nach dem gcd von 12x und 6. 6 ist die größte Zahl, die sowohl 12x als auch 6 teilt, also können wir die Gleichung auf 6(2x + 1) vereinfachen. Dieser Vorgang gilt auch für Gleichungen mit negativen Zahlen und Brüchen. x/2 + 4 kann zum Beispiel zu 1/2(x + 8) vereinfacht werden und -7x + -21 kann in -7(x + 3) eingerechnet werden. 

Nehmen wir zum Beispiel die quadratische Gleichung x + 5x + 6 = 0. Da 3 x 2 = 6 und 3 + 2 = 5 ist, wird die vereinfachte Gleichung (x + 3)(x + 2). Leichte Variationen dieser einfachen Schnelllösung finden Sie in der Gleichung selbst: Wenn die quadratische Gleichung die Form x-bx+c hat, sieht Ihre Antwort so aus: (x - _)(x - _). Wenn von der Form x+bx+c, dann sieht Ihre Antwort so aus: (x + _)(x + _). In der Form x-bx-c sieht Ihre Antwort so aus: (x + _)(x - _). Hinweis: Die Leerzeichen können Brüche oder Dezimalzahlen sein. Zum Beispiel die Gleichung x + (21/2)x + 5 = 0 Faktoren in (x + 10)(x + 1/2). 
Lassen Sie uns eine Beispielaufgabe erarbeiten. 3x - 8x + 4 wirkt zunächst etwas einschüchternd. Aber wenn wir erkennen, dass 3 nur zwei Faktoren (3 und 1) hat, dann wird es viel einfacher, weil wir wissen, dass unsere Antwort die Form (3x +/- _)(x +/- _) haben muss. In diesem Fall ergibt die Eingabe von -2 in die Lücken die richtige Antwort. -2 × 3x = -6x und -2 × x = -2x. -6x + -2x = -8x. -2 × -2 = 4, also sehen wir, dass die in Klammern multiplizierten Terme die ursprüngliche Gleichung als Produkt haben. 
Zum Beispiel erfüllt die Gleichung x + 6x + 9 diese Form. 3 ist 9 und 3 × 2 ist 6. Wir wissen also, dass die Faktoren dieser Gleichung gleich (x + 3)(x + 3) oder (x + 3) sind. 
Kehren wir zur Gleichung x + 5x + 6 = 0 . zurück. Die gelöste Gleichung lautet (x + 3)(x + 2) = 0. Wenn einer dieser Faktoren gleich 0 ist, dann ist die ganze Gleichung 0, also sind die möglichen Antworten für x die Zahlen, bei denen (x + 3) und (x + 2) gleich 0 . sind. Diese Zahlen sind -3 bzw. -2. 
Wir wenden -2 und -3 auf x + 5x + 6 = 0 . an. Zuerst: -2: (-2) + 5(-2) + 6 = 0 4 + -10 + 6 = 0 0 = 0. Das ist richtig, also ist -2 eine gültige Antwort. Jetzt versuchen wir -3: (-3) + 5(-3) + 6 = 0 9 + -15 + 6 = 0 0 = 0. Das ist auch richtig, also ist -3 auch eine gültige Antwort. 

Die Gleichung 4x + 8xy + 4y kann umgeschrieben werden als 4x + (2 × 2 × 2)xy + 4y. Jetzt wird klar, dass es in der richtigen Form ist, sodass wir mit einiger Sicherheit sagen können, dass unsere Gleichung in (2x + 2y) eingerechnet werden kann. 
Zum Beispiel: 8x - 27y können berücksichtigt werden (2x - 3y)(4x + ((2x)(3y)) + 9y).
Faktorisieren von gleichungen
In der Mathematik ist es faktorisieren Bestimmen von Zahlen oder Ausdrücken, die, wenn sie miteinander multipliziert werden, einen bestimmten Wert oder eine bestimmte Gleichung ergeben. Faktorisieren ist eine nützliche Fähigkeit, die man beim Lösen einfacher mathematischer Probleme erlernen kann. die Fähigkeit, richtig zu faktorisieren, wird beim Umgang mit quadratischen Gleichungen und anderen Polynomen fast unerlässlich. Faktorisieren kann verwendet werden, um einfache mathematische Gleichungen zu vereinfachen, um sie leichter lösen zu können. Durch Factoring können Sie mögliche Antworten viel schneller selbst ausschließen, als wenn Sie jede einzelne von ihnen prüfen müssten.
Schritte
Methode 1 von 3: Faktorisieren von Zahlen und einfachen Gleichungen

1. Verstehen Sie die Definition des Faktorisierens in Zahlen. Faktorisieren ist im Prinzip einfach, aber in der Praxis kann es beim Lösen komplexer Gleichungen ziemlich schwierig sein. Daher ist der einfachste Ansatz, mit kleinen Zahlen und dann einfachen Gleichungen zu beginnen, bevor Sie zu fortgeschritteneren Anwendungen übergehen. Der Faktoren einer bestimmten Zahl sind die Zahlen, die miteinander multipliziert diese einzelne Zahl ergeben. Die Faktoren von 12 sind beispielsweise 1, 12, 2, 6, 3 und 4, weil 1 × 12, 2 × 6 und 3 × 4 alle 12 als Produkt haben.
- Eine andere Möglichkeit, sich das vorzustellen, ist, dass die Faktoren einer gegebenen Zahl diejenigen Zahlen sind, die die Zahl in kann komplett geteilt werden.
- Können Sie alle Faktoren von 60 . finden?? Wir verwenden die Zahl 60 für verschiedene Anwendungen (die Anzahl der Minuten in einer Stunde, Sekunden in einer Minute usw.).), weil es durch eine große Menge von Zahlen teilbar ist.
- Die Faktoren von 60 sind 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 und 60.

2. Verstehe, dass Gleichungen auch faktorisiert werden können. Genau wie Zahlen können auch Variablen mit Koeffizienten faktorisiert werden. Sie tun dies, indem Sie die Faktoren des Koeffizienten der Variablen ermitteln. Zu wissen, wie man Variablen faktorisiert, ist hilfreich, um Gleichungen zu vereinfachen, zu denen die Variablen gehören.

3. Wenden Sie die Verteilungseigenschaft der Multiplikation an, um mathematische Gleichungen zu faktorisieren. Mit Ihrem Wissen, wie man sowohl reguläre Zahlen als auch Variablen mit Koeffizienten faktorisiert, können Sie mathematische Gleichungen auch vereinfachen, indem Sie die Faktoren bestimmen, die Zahlen und Variablen in einer mathematischen Gleichung gemeinsam haben. Normalerweise vereinfachen wir die Gleichung so weit wie möglich, indem wir nach dem größten gemeinsamen Teiler (gcd) suchen. Dieser Vereinfachungsprozess ist wegen der Verteilungseigenschaft der Multiplikation möglich, die besagt, dass für jede Zahl a, b und c, a(b + c) = ab + ac.
Methode 2 von 3: Quadratische Gleichungen faktorisieren

1. Stellen Sie sicher, dass die Gleichung quadratisch ist (ax + bx + c = 0). quadratische Gleichungen haben die Form ax + bx + c = 0, wobei a, b und c numerische Konstanten sind und a ungleich 0 ist (beachten Sie, dass a gleich kann sind auf 1 oder -1). Wenn Sie es mit einer Gleichung mit einer Variablen (x) und einem oder mehreren Termen von x zum Quadrat zu tun haben, können Sie die Terme der Gleichung normalerweise mit einer mathematischen Standardoperation vertauschen, um auf einer Seite der Gleichung 0 zu erhalten Zeichen und Axt usw. auf der anderen Seite.
- Sie haben zum Beispiel die folgende mathematische Gleichung: 5x + 7x - 9 = 4x + x - 18, die in der quadratischen Form zu x + 6x + 9 = 0 vereinfacht werden kann.
- Gleichungen mit größeren Potenzen von x, wie x, x usw. sind keine quadratischen Gleichungen. Dies sind kubische Gleichungen oder höher, es sei denn, die Gleichung kann so vereinfacht werden, dass die Terme mit höheren Potenzen von x (als Quadraten) eliminiert werden.

2. In quadratischen Gleichungen mit a = 1 berücksichtigen Sie (x+d )(x+e), wobei d × e = c und d + e = b. Wenn Ihre quadratische Gleichung die Form x + bx + c = 0 hat (mit anderen Worten, wenn der Koeffizient von x = 1), dann ist es möglich (aber nicht sicher), dass eine relativ einfache Abkürzung zum Faktorisieren der Gleichung verwendet werden kann. Finde zwei Zahlen, die beide c als Produkt haben und addiere sie zusammen, um b als Summe zu erhalten. Wenn Sie diese beiden Zahlen d und e haben, setzen Sie sie in den folgenden Ausdruck ein: (x+d)(x+e). Diese beiden Terme ergeben, wenn sie multipliziert werden, die quadratische Gleichung - mit anderen Worten, sie sind die Faktoren Ihrer quadratischen Gleichung.

3. Wenn möglich kann man die Faktoren auch durch genaues Hinsehen auflösen. Ob Sie es glauben oder nicht, Sie können einfache quadratische Gleichungen lösen, indem Sie sich das Problem genau ansehen und dann die möglichen Antworten abwägen, bis Sie die richtige gefunden haben. Mit anderen Worten, durch Ausprobieren in Faktoren zerlegen. Hat die Gleichung die Form ax+bx+c und a>1, dann haben die Terme die Form (dx +/- _)(ex +/- _), wobei d und e Konstanten größer Null sind, die zusammen multipliziert a als Produkt ergeben. Sowohl d als auch e (oder beide) kann gleich 1, aber das ist nicht immer so. Wenn beide 1 sind, haben Sie im Wesentlichen die oben beschriebene Schnellmethode verwendet.

4. Lösen Sie dies durch Quadrieren. In manchen Fällen können quadratische Gleichungen schnell und einfach faktorisiert werden, indem eine spezielle mathematische Eigenschaft verwendet wird. Jede quadratische Gleichung der Form x + 2xh + h = (x + h). Wenn also in Ihrer Gleichung der Wert für b das Doppelte der Quadratwurzel von c ist, kann Ihre Gleichung in (x + (sqrt(c))) eingerechnet werden.

5. Verwenden Sie Faktoren, um quadratische Gleichungen zu lösen. Unabhängig davon, wie Sie eine quadratische Gleichung faktorisieren; Sobald es berücksichtigt ist, können Sie die möglichen Antworten für den Wert für x finden, indem Sie jeden Faktor auf Null setzen und danach auflösen. Da Sie nach Werten für x suchen, bei denen Ihre Gleichung Null ist, ist ein Wert für x, der einen der beiden Faktoren gleich Null macht, die mögliche Antwort Ihrer quadratischen Gleichung.

6. Überprüfen Sie Ihre Antworten – einige davon können falsch sein! Sobald Sie die möglichen Antworten für x gefunden haben, wenden Sie sie wieder auf Ihre ursprüngliche Gleichung an, um zu sehen, ob sie gültig sind. Manchmal sind die Antworten, die Sie finden, die ursprüngliche Gleichung nicht mache gleich null, wenn du sie anwendest. Diese Antworten sind falsch und wir ignorieren sie.
Methode 3 von 3: Faktorisieren anderer Gleichungsformen

1. Wenn die Gleichung die Form a-b hat, sind die faktorisierten Terme (a+b)(a-b). Gleichungen zweier Variablen werden anders aufgelöst als quadratische Gleichungen. Für jede Gleichung a-b, bei der a und b ungleich 0 sind, sind die Faktoren der Gleichung (a+b)(a-b).
- Zum Beispiel die Gleichung 9x - 4y = (3x + 2y)(3x - 2y).

2. Wenn die Gleichung die Form a+2ab+b hat, zerlege sie in (a+b). Hinweis: mit a das Trinom der Form a-2ab+b, die aufgelöste Form ist etwas anders: (a-b).

3. Hat die Gleichung die Form a-b, dann zerlegst du sie in (a-b)(a+ab+b). Abschließend sei noch erwähnt, dass auch kubische Gleichungen und höhere Polynome faktorisiert werden können, allerdings wird dieser Vorgang schnell unausführbar.
Tipps
- a-b kann faktorisiert werden, aber a+b nicht.
- Lernen Sie, Konstanten zu faktorisieren – das kann helfen.
- Achte bei der Faktorisierung auf Brüche und bearbeite sie richtig und sorgfältig.
- Wenn Sie ein Trinom der Form x+bx+ (b/2) haben, dann ist die faktorisierte Form (x+(b/2)) (Sie können dies mit einer Quadratformel begegnen).
- Denken Sie daran, dass a x 0 = 0.
Notwendigkeiten
- Papier
- Bleistift
- Mathebuch (bei Bedarf)
"Faktorisieren von gleichungen"
Оцените, пожалуйста статью