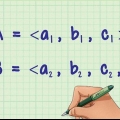Anteilsberechnung: 7 Schritte (mit Bildern)

Schritte
- Teil 1 von 2: Verhältnis schreiben
- Teil 2 von 2: Verhältniszahlen in mathematischen Aufgaben verwenden
Beispielübungen
Tipps
Notwendigkeiten

Proportionen oder Verhältnisse sind mathematische Ausdrücke, die zwei oder mehr Zahlen vergleichen. Proportionen können feste Mengen und Zahlen vergleichen oder kann verwendet werden, um Teile des Ganzen zu vergleichen. Proportionen können auf unterschiedliche Weise berechnet und notiert werden, aber die Prinzipien sind für alle Quotienten gleich. Siehe Schritt 1 unten, um mit Proportionen zu beginnen.

Schritte

Teil 1 von 2: Verhältnis schreiben

1. Verstehen Sie, wie Proportionen verwendet werden. Beziehungen findet man überall, in der wissenschaftlichen Welt oder zu Hause. Die einfachsten Verhältnisse vergleichen nur zwei Werte, aber mehr geht natürlich auch.

Ein Beispiel: In einer Klasse mit 20 Schülern, davon 5 Mädchen und 15 Jungen, können wir die Zahl der Mädchen und Jungen ins Verhältnis setzen.

2. Schreiben Sie ein Verhältnis mit einem Doppelpunkt. Eine übliche Methode, ein Verhältnis anzugeben, ist ein Doppelpunkt zwischen den Zahlen. Wenn Sie zwei Zahlen vergleichen, schreiben Sie es zum Beispiel als 7 : 13 auf und wenn es 3 oder mehr Zahlen gibt, dann zum Beispiel wie folgt 10 : 2 : 23.

Somit können wir in unserem Klassenzimmer das Verhältnis von Mädchen zu Jungen wie folgt schreiben:5 Mädchen : 15 Jungen. Sie können die Bezeichnung optional weglassen, solange Sie sich daran erinnern, wofür das Verhältnis steht.

3. Ein Verhältnis ist gleich einem Bruch und kann daher vereinfacht werden. Sie tun dies, indem Sie alle Terme des Verhältnisses durch die gemeinsamen Teiler dividieren, bis keine gemeinsamen Teiler mehr übrig sind. Aber wenn Sie dies tun, ist es wichtig, nicht zu vergessen, was die ursprünglichen Zahlen des Verhältnisses waren. Siehe unten.

Im Klassenzimmerbeispiel waren es 5 Mädchen und 15 Jungen. Beide Seiten des Verhältnisses sind durch 5 . teilbar. Dadurch können Sie das Verhältnis zu vereinfachen1 Mädchen: 3 Jungen.

Aber wir sollten die Originalzahlen nicht aus den Augen verlieren. Es sind nicht 4, sondern insgesamt 20 Schüler in der Klasse. Das vereinfachte Verhältnis vergleicht nur das Verhältnis zwischen der Anzahl der Jungen und Mädchen. Es gibt 3 Jungen zu 1 Mädchen im Verhältnis oder Bruchteil, nicht 3 Jungen und 1 Mädchen in der Klasse.

Einige Proportionen können nicht vereinfacht werden. Zum Beispiel kann 3 : 56 nicht vereinfacht werden, weil die 2 Zahlen keine gleichen Faktoren haben - 3 ist eine Primzahl und 56 ist nicht durch 3 teilbar.

4. Es gibt auch alternative Methoden zum Schreiben von Proportionen. Während der Doppelpunkt vielleicht am einfachsten zum Schreiben von Verhältnissen ist, gibt es andere Möglichkeiten, die das Verhältnis nicht beeinflussen. Siehe unten:

Proportionen können auch angezeigt werden als "3 steht bis 6" oder "11 auf 4 auf 20".

Sie können Proportionen auch als Bruch schreiben. Oft führt die Verwendung beider Begriffe zu Verwirrung, aber Brüche sind Proportionen und umgekehrt. Du kannst also auch ein Verhältnis mit einer Teilungslinie schreiben. Zum Beispiel das Verhältnis 3/5 und der Bruch 3/5 unterscheiden sich nicht voneinander. Wie im Beispiel der Klasse: Auf jedes Mädchen kamen 3 Jungen, im Verhältnis 1 : 3, aber als Bruchteil drückt das gleiche aus, nämlich 1/3 der Gesamtzahl der Schüler ist ein Mädchen.

Teil 2 von 2: Verhältniszahlen in mathematischen Aufgaben verwenden

1. Verwenden Sie Multiplikation oder Division, um Verhältnisse zu ändern, ohne das Verhältnis zu ändern. Das Multiplizieren oder Dividieren beider Terme eines Verhältnisses mit einer gegebenen Zahl ergibt das gleiche Verhältnis, jedoch mit größeren oder kleineren Zahlen.

Angenommen, Sie sind Lehrer und sollen die Klasse um das Fünffache erhöhen, jedoch mit dem gleichen Verhältnis von Jungen und Mädchen. Wenn jetzt 8 Mädchen und 11 Jungen in der Klasse sind, wie viele sind in der neuen Klasse??Lesen Sie weiter für die Lösung:

8 Mädchen und 11 Jungen, also ein Verhältnis von 8 : 11. Dieses Verhältnis weist also darauf hin, dass es unabhängig von der Klassengröße 8 Mädchen zu 11 Jungen gibt.
(8 : 11) × 5
(8×5 : 11×5)
(40:55). Die neue Klasse besteht aus 40 Mädchen und 55 Jungs - 95 Schüler insgesamt!

2. Verwenden Sie die Kreuzmultiplikation, um die unbekannte Variable zu finden, wenn Sie mit zwei äquivalenten Verhältnissen arbeiten. Ein weiteres bekanntes Problem besteht darin, dass Sie aufgefordert werden, die Unbekannte eines Verhältnisses zu berechnen. Kreuzmultiplikation macht dies sehr einfach. Schreiben Sie jedes Verhältnis als Bruch, machen Sie sie gleich und multiplizieren Sie kreuzweise, um zu lösen.

Nehmen wir als Beispiel an, wir haben eine Schülergruppe von 2 Jungen und 5 Mädchen. Wenn wir das Verhältnis intakt halten wollen, wie viele Jungen sind in einer Gruppe von 20 Mädchen??Um dies zu lösen, machen wir zwei Verhältnisse, eines mit der unbekannten Variablen: 2 Jungen : 5 Mädchen = x Jungen : 20 Mädchen. In Bruchform sieht es so aus: 2/5 = x/20. Verwenden Sie Kreuzmultiplikation, um dies zu lösen. Siehe unten:

2/5 = x/20

5 × x = 2 × 20

5x = 40

x = 40/5 = 8. Es sind also 20 Mädchen und 8 Jungs.

3. Verwenden Sie Verhältnisse, um unbekannte Größen zu finden, bei denen eine andere gegeben ist. Wenn Sie es mit einer Variablen zu tun haben, die die Beziehung zwischen mehreren Größen bestimmt, von denen eine oder mehrere unbekannt sind, können Sie den Wert jeder Unbekannten mit nur einer bekannten Größe ermitteln. Bei solchen Aussagen geht es oft darum, die Mengen der Zutaten in einem Rezept zu berechnen. Um die unbekannten Größen zu finden, dividiere den bekannten Term des Verhältnisses durch die gegebene Größe; danach teilen jeder Term im Verhältnis nach der antwort, die du bekommst. Ein Beispiel soll es etwas klarer machen:

Angenommen, unsere Klasse backt Kekse als Aufgabe. Wenn das Teigrezept aus Mehl, Wasser und Butter im Verhältnis 20 : 8 : 4 besteht und jeder Schüler 5 Tassen Mehl erhält; Wie viel Wasser und Butter braucht jeder Schüler?? Um dies zu lösen, teilen Sie zuerst den Term des dem bekannten Verhältnis entsprechenden Verhältnisses (20) durch die bekannte Menge (5 Tassen). Dann dividiere jeden Term im Verhältnis durch die Antwort, die du erhältst, um den genauen Betrag für jeden zu finden. Siehe unten:

20 / 5 = 4

20/4 : 8/4 : 4/4

5 : 2 : 1. So, 5 Tassen Mehl, 2 Tassen Wasser und 1 Tasse Butter.

Beispielübungen

Kekse bestehen aus Butter und Zucker im Verhältnis 5:3. Wenn 7 Teile Butter verwendet werden, wie viel Zucker wird benötigt?

Verwenden Sie dazu das Verhältnis in Form eines Bruchs. In diesem Fall machen wir eine Dezimalzahl – ungefähr 1,67.
Die Formel ist jetzt einsatzbereit. Wir wollen die Zuckermenge ermitteln, also belassen wir es bei dem was es ist und berechnen den Anteil Butter/1,67, also 7/1,67 = 4,192

Der Teil, der sich mit Proportionen befasst, ist proportionales Dividieren. Wenn eine Gesamtmenge in Teile geteilt wird, wird ein Verhältnis erstellt. Zum Beispiel: Annemiek, Anna und Anton arbeiten alle im Laden ihrer Mutter. Annemiek arbeitete eine Stunde, Anna 3 und Anton 6 Stunden (also ein Verhältnis von 1:3:6). Die Mutter gibt ihnen einen Gesamtbetrag und bittet sie, diesen selbst im richtigen Verhältnis aufzuteilen. Der Gesamtbetrag betrug 100 €. Sie tun dies, indem Sie die Teile des Verhältnisses zusammenzählen, damit Sie wissen, wie viel jeder Teil wert ist. 1:3:6 wird dann zu 1+3+6=10, also $100/10=$10, also wissen wir jetzt, dass jeder Teil des Verhältnisses $10 wert ist... und deshalb bekommt jeder einen Lohn von 10€ pro Stunde. Jetzt können wir damit berechnen, was jeder verdient hat. Annemiek bekommt 10 €, Anna 30 € und Anton 60 €. Überprüfen Sie dies, indem Sie alle Löhne addieren, die 100 € ergeben sollten. 10+30+60= 100. Richtig!

Tipps

Vereinfachen Sie Verhältnisse, indem Sie die ab/c-Taste auf Ihrem Taschenrechner verwenden (dies dient zum Schreiben von gemischten Brüchen und zum Vereinfachen). Wenn Sie beispielsweise 8:12 haben, testen Sie "8 ab/c 12" = in und Sie erhalten 2/3, und damit das Verhältnis 2:3.