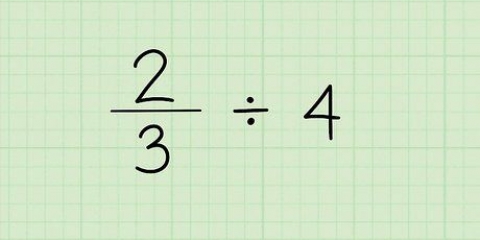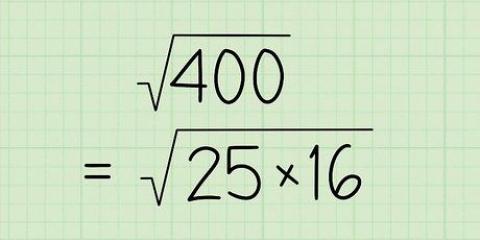Kostenlose Schritt für Schritt Anweisungen 
Die einzige Ausnahme von dieser Regel ist die Zahl 2 selbst, die, weil sie durch sich selbst und 1 teilbar ist, auch eine Primzahl ist. 2 ist die einzige gerade Primzahl. 
Wenn wir zum Beispiel diese Methode verwenden wollten, um zu testen, ob 11 eine Primzahl ist oder nicht, müssten wir 11 durch 3, 4, 5, 6, 7, 8, 9 und 10 teilen und jedes Mal nach einer ganzzahligen Antwort suchen ohne Rest. Da keine dieser Zahlen vollständig in 11 passt, können wir sagen, dass 11 a . ist Primzahl ist. 
Untersuchen wir die Faktoren von 100. 100 = 1 × 100, 2 × 50, 4 × 25, 5 × 20, 10 × 10, 20 × 5, 25 × 4, 50 × 2 und 100 × 1. Beachten Sie, dass nach 10 × 10 die Faktoren die gleichen wie für 10 × 10 sind, nur umgekehrt. Im Allgemeinen können wir die Faktoren von n größer als sqrt(n) ignorieren, da sie einfach eine Fortsetzung von Faktoren kleiner als sqrt(n) sind. Versuchen wir es mit einem Beispiel. Wenn n = 37, dann müssen wir nicht alle Zahlen von 3 bis 36 testen, um zu bestimmen, ob n eine Primzahl ist. Stattdessen müssen wir uns nur die Zahlen zwischen 2 und sqrt(37) ansehen (aufgerundet). Quadrat (37) = 6.08 – wir werden dies auf 7 . aufrunden. 37 ist nicht vollständig durch 3, 4, 5, 6 und 7 teilbar und daher können wir mit Sicherheit sagen, dass es a . ist Primzahl ist. 
Das bedeutet, dass alle geraden Faktoren sowie solche, die Vielfache von Primzahlen sind, übersprungen werden können. Versuchen wir zum Beispiel festzustellen, ob 103 eine Primzahl ist oder nicht. Die Quadratwurzel von 103 ist 11 (aufgerundet). Die Primzahlen zwischen 2 und 11 sind 3, 5, 7 und 11. 4, 6, 8 und 10 sind gerade und 9 ist ein Vielfaches von 3, eine Primzahl, also können wir diese überspringen. Dadurch haben wir unsere Liste möglicher Faktoren auf nur 4 Zahlen reduziert! 103 ist nicht vollständig durch 3, 5, 7 oder 11 teilbar, daher wissen wir jetzt, dass 103 a . ist Primzahl ist. 
Ein Beispiel: Ist 100 eine Primzahl oder nicht?. Angenommen, wir nehmen 3 als Testwert - dieser liegt zwischen 2 und n-1, das reicht also. 
Eine andere Methode besteht darin, a zu berechnen, dann durch n zu dividieren und dann den Rest als Antwort zu verwenden. Spezielle Taschenrechner mit einer Modulusfunktion können beim Dividieren großer Zahlen sehr nützlich sein, da sie den Rest einer Division direkt berechnen können. Wenn wir in unserem Beispiel einen solchen Rechner verwenden, können wir sehen, dass 3/100 einen Rest von 1 . hat. 3 (mod 100) ist also 1. 
In unserem Beispiel berechnen wir 3 mit einem Modul von 100. 3 ist eine sehr, sehr große Zahl - 515.377.520.732.011.331.036.461.129.765.621.272.702.107.522.001 - so groß, dass es sehr schwierig wird, damit zu arbeiten. Anstatt die 48-stellige Antwort für 3 zu verwenden, schreiben wir sie besser als Exponenten, also ((((((((3)*3))))*3)). Denken Sie daran, dass das Nehmen des Exponenten eines Exponenten den Effekt einer Multiplikation der Exponenten ergibt ((x) = x). Jetzt können wir den Rest bestimmen. Beginnen Sie mit der Auflösung nach (((((((3)*3))))*3)) am inneren Satz von Klammern und arbeiten Sie sich heraus, indem Sie jeden Schritt durch 100 . teilen. Sobald wir den Rest gefunden haben, verwenden wir ihn für den nächsten Schritt anstatt als eigentliche Antwort. Siehe unten: (((((((9)*3))))*3)) - 9/100 hat keinen Rest, also können wir fortfahren. ((((((27))))*3)) - 27/100 hat keinen Rest, also können wir fortfahren. (((((729)))*3)) - 729/100 = 7 R 29. Unser Rest ist 29. Wir gehen zum nächsten Schritt über, nicht 729. ((((29=841))*3)) - 841/100 = 8 R 41. Unsere restlichen 41 werden wir im nächsten Schritt wieder verwenden. (((41 = 1681)*3)) - 1681/100 = 16 R 81. Wir werden unseren Rest 81 im nächsten Schritt verwenden. ((81*3 = 243)) - 243/100 = 2 R 43. Wir werden unsere restlichen 43 im nächsten Schritt verwenden. (43 = 1849) - 1849/100 = 18 R 49. Wir werden unsere restlichen 49 im nächsten Schritt verwenden. 49 = 2401 - 2401/100 = 24 R 1. unser letzter Rest ist 1. Mit anderen Worten, 3 (mod 100) = 1. Beachten Sie, dass dies dieselbe Antwort ist, die wir im vorherigen Schritt berechnet haben! 
In unserem Beispiel 3 (mod 100) = 1 und 3 (mod 100) = 3. 1 ≠ 3, also können wir sagen, dass 100 eine zusammengesetzte Zahl ist. 
Angenommen, wir wollen bestimmen, ob n = 321 eine Primzahl ist. 321 - 1 = 320, was wir ausdrücken können als 2×5. In diesem Fall ist n = 321 eine geeignete Zahl. Die Bestimmung von n – 1 für n = 371 kann einen großen Wert für d erfordern, was den gesamten Prozess zu einem späteren Zeitpunkt erschwert. 371 - 1 = 370 = 2 × 185 
In unserem Beispiel mit n = 321 wählen wir a = 100. 
In unserem Beispiel mit n = 321 a (mod n) = 100 (mod 321). 100 = 10.000.000.000 (mod 321) = 313. Wir verwenden einen speziellen Taschenrechner oder die Abkürzungsmethode mit einem Exponenten, wie oben beschrieben, um den Rest von 100/321 . zu finden. Da wir weder 1 noch -1 erhalten haben, können wir nicht mit Sicherheit sagen, dass n eine Primzahl ist. Aber wir müssen noch mehr tun – lesen Sie weiter. 
Zur Erinnerung, in unserem Beispiel ist der Wert von a gleich 100, der Wert von s ist 6 und von d5. Wir werden mit den Tests wie unten angegeben fortfahren: 100 = 1×10. 1×10 (mod 321) = 64. 64 ` 1 oder -1. Ruhig halten. 100 = 1×10. 1×10 (mod 321) = 244. 244 ≠ 1 oder -1. An dieser Stelle können wir aufhören. s - 1 = 6 - 1 = 5. Wir haben nun 4d = 2 erreicht, und es gibt keine Potenzen von 2 mal d unter 5d. Da keine unserer Berechnungen eine 1 oder -1 als Antwort ergab, können wir sagen, dass n = 321 a zusammengesetzt Nummer ist. 
Daten1 = 1 Daten2 = 2 
Berechnen Sie den MMI MMI1 = Testnummer2 ^ -1 Mod Testnummer1 MMI2 = Testnummer1 ^ -1 Mod Testnummer2 Nur für Primzahlen (es wird ein Ergebnis für Nicht-Primzahlen geben, aber das ist nicht das MMI): MMI1 = (Testnummer2 ^ (Testnummer1-2)) %Testnummer1 MMI2 = (Testnummer1 ^ (Testnummer-2)) % Testnummer2 So: MMI1 = (97^33) %35 MMI2 = (35^95) %97 
Für das MMI1 F(1) = Testnummer2 % Testnummer1 = 97 % 35 = 27 F(2) = F(1) * F(1) % Testnummer1 = 27 * 27 % 35 = 29 F(4) = F(2) * F(2) % Testnummer1 = 29 * 29 % 35 = 1 F(8) = F(4) * F(4) % Testnummer1 = 1 * 1 % 35 = 1 F(16) =F(8) * F(8) % Testnummer1 = 1 * 1 % 35 = 1 F(32) = F(16) * F(16) % Testnummer1 = 1 * 1 % 35 = 1 Berechnen Sie den binären Logarithmus von Testnummer1 - 2 35 -2 = 33 (10001) Basis 2 MMI1 = F(33) = F(32) * F(1) mod 35 MMI1 = F(33) = 1 * 27 Mod 35 MMI1 = 27 Für MMI2 F(1) = Testnummer1 % Testnummer2 = 35 % 97 = 35 F(2) = F(1) * F(1) % Testnummer2 = 35 * 35 mod 97 = 61 F(4) = F(2) * F(2) % Testnummer2 = 61 * 61 mod 97 = 35 F(8)= F(4) * F(4) % Testnummer2 = 35 * 35 mod 97 = 61 F(16) = F(8) * F(8) % Testnummer2 = 61 * 61 mod 97 = 35 F(32)= F(16) * F(16) % Testnummer2 = 35 * 35 mod 97 = 61 F(64)= F(32) * F(32) % Testnummer2 = 61 * 61 mod 97 = 35 F(128) = F(64) * F(64) % Testnummer2 = 35 * 35 mod 97 = 61 Berechnen Sie den binären Logarithmus von TestNumber2 - 2 97 - 2 = 95 = (1011111) Basis 2 MMI2 = (((((F(64) * F(16) % 97) * F(8) % 97) * F(4) % 97) * F(2) % 97) * F(1) % 97 ) MMI2 = (((((((35 * 35) %97) * 61) % 97) * 35 % 97) * 61 % 97) * 35 % 97) MMI2 = 61 
Antwort = (1 * 97 * 27 + 2 * 35 * 61) % (97 * 35) Antwort = (2619 + 4270) % 3395 Antwort = 99 
Berechnen (Antwort - Daten1) % Testnummer1 99 -1 % 35 = 28 Da 28 größer als 0 ist, ist 35 keine Primzahl 
Berechnen (Antwort - Daten2) % Testnummer2 99 - 2% 97 = 0 Da 0 gleich 0 ist, ist 97 eine potentielle Primzahl 
Wenn Schritt 7 gleich 0 ist: Benutze einen anderen "Testnummer1" wenn TestNummer1 keine Primzahl ist. Verwenden Sie eine andere Testnummer1, wobei eine Testnummer1 tatsächlich eine Primzahl ist.In diesem Fall sind die Schritte 6 und 7 gleich 0. Verwenden Sie unterschiedliche Datenpunkte für data1 und data2. Wenn Schritt 7 immer gleich 0 ist, dann ist die Wahrscheinlichkeit, dass Zahl2 eine Primzahl ist, sehr hoch. Es ist bekannt, dass die Schritte 1 bis 7 in bestimmten Fällen falsch sind, wenn die erste Zahl keine Primzahl ist und die zweite ein Primfaktor der Nichtprimzahl ist "Testnummer1".Es funktioniert in allen Szenarien, in denen beide Zahlen Primzahlen sind. Der Grund, warum die Schritte 1 bis 7 wiederholt werden, liegt darin, dass es einige Szenarien gibt, in denen, selbst wenn TestNumber1 keine Primzahl und TestNumber2 keine Primzahl ist, eine der Zahlen aus Schritt 7 immer noch Null ist.Diese Bedingungen sind selten.Durch Ändern von TestNumber1 in eine andere nicht Primzahl wird TestNumber2 in Schritt 7 nicht mehr gleich Null, wenn TestNumber2 keine Primzahl ist. Mit Ausnahme des Falles, in dem "Testnummer1" ist ein Faktor von TestNumber2, Primzahlen sind in Schritt 7 immer Null.
Prüfe, ob eine zahl eine primzahl ist
Primzahlen sind Zahlen, die nur durch sich selbst teilbar sind und heißen 1 – andere Zahlen Verbindung Zahlen. Um zu testen, ob eine Zahl eine Primzahl ist, gibt es mehrere Möglichkeiten. Einige dieser Methoden sind relativ einfach, aber für größere Zahlen definitiv nicht praktikabel. Andere häufig verwendete Tests sind tatsächlich vollständige Algorithmen basierend auf a Wahrscheinlichkeit die manchmal eine Zahl fälschlicherweise als Primzahl klassifizieren. Lesen Sie bei Schritt 1 weiter, um zu erfahren, wie Sie sich selbst testen können, wenn Sie es mit einer Primzahl zu tun haben.
Schritte
Methode 1 von 4: Versuchen Sie es durch Teilen
Der Versuch durch Teilen ist bei weitem der einfachste Weg, eine Zahl zu testen. Bei kleinen Zahlen ist es meist auch der schnellste Weg. Der Test basiert auf der Definition einer Primzahl: Eine Zahl ist prim, wenn sie nur durch sich selbst teilbar ist und 1.
1. Paar n ist die Nummer, die Sie testen möchten. Dividiere die Zahl n durch alle möglichen teilbaren ganzen Zahlen. Bei größeren Zahlen wie n=101 ist es äußerst unpraktisch, durch jede mögliche ganze Zahl kleiner als n . zu dividieren. Glücklicherweise gibt es mehrere Tricks, um die Anzahl der zu testenden Faktoren zu reduzieren.
2. Herausfinden, ob n sogar ist. Alle geraden Zahlen sind vollständig durch 2 . teilbar. Wenn n gerade ist, können Sie also sagen, dass n ist eine zusammengesetzte Zahl (und daher keine Primzahl). Um schnell festzustellen, ob eine Zahl gerade ist, musst du nur auf die letzte Ziffer achten. Wenn die letzte Ziffer 2, 4, 6, 8 oder 0 ist, ist die Zahl gerade und nicht prim.
3. Teil n um eine beliebige Zahl zwischen 2 und n-1. Da eine Primzahl keine anderen Faktoren außer sich selbst und 1 hat und weil Faktoren von ganzen Zahlen kleiner als ihr Produkt sind, wird die Prüfung der Teilbarkeit einer ganzen Zahl kleiner als n und größer als 2 feststellen, ob n eine Primzahl ist. Wir beginnen nach 2, weil gerade Zahlen (Vielfache von 2) keine Primzahlen sein können. Dies ist alles andere als eine effiziente Methode zum Testen, wie Sie unten sehen werden.
4. Um Zeit zu sparen, testen Sie nur bis zu sqrt(n), aufgerundet. Das Testen einer Zahl n durch Prüfen aller Zahlen zwischen 2 und n-1 kann schnell sehr zeitaufwändig werden. Wenn wir beispielsweise mit dieser Methode überprüfen wollten, ob 103 eine Primzahl ist, müssten wir durch 3, 4, 5, 6, 7 . dividieren ... etc., bis 102! Zum Glück ist es nicht notwendig, so zu testen. In der Praxis ist es nur notwendig, mit den Faktoren zwischen 2 und der Quadratwurzel von n . zu testen. Wenn die Quadratwurzel von n keine Zahl ist, runden Sie sie auf die nächste ganze Zahl und testen Sie auf diese Zahl. Siehe unten für eine Erklärung:
5. Um noch mehr Zeit zu sparen, verwenden wir nur Primfaktoren. Es ist möglich, den Prozess des Testens durch Division noch kürzer zu machen, indem die Faktoren, die keine Primzahlen sind, nicht berücksichtigt werden. Per Definition kann jede zusammengesetzte Zahl als das Produkt von zwei oder mehr Primzahlen ausgedrückt werden. Es ist also unnötig, die Zahl n durch eine zusammengesetzte Zahl zu teilen - dies entspricht einer mehrfachen Division durch Primzahlen. Wir können die Liste der möglichen Faktoren also weiter auf Primzahlen kleiner als sqrt(n) eingrenzen.
Methode 2 von 4: Den kleinen Satz von Fermat verwenden
1640 stellte der französische Mathematiker Pierre de Fermat erstmals einen Satz auf (der heute nach ihm benannt ist), der sehr hilfreich sein kann, um zu bestimmen, ob eine Zahl eine Primzahl ist oder nicht. Technisch gesehen soll der Fermat-Test prüfen, ob eine Zahl zusammengesetzt und nicht prim ist. Dies liegt daran, dass der Test mit "Absolute Sicherheit" kann zeigen, dass eine Zahl zusammengesetzt ist, aber nur a "Wahrscheinlichkeit" ob eine Zahl eine Primzahl ist. Der kleine Satz von Fermat ist in Situationen nützlich, in denen der Versuch einer Division durch nicht praktikabel ist und wenn eine Liste von Zahlen verfügbar ist, die Ausnahmen vom Satz darstellen.
1. Vermuten n die nummer ist zum testen. Mit diesem Test ermitteln Sie, ob eine gegebene Zahl n eine Primzahl ist. Aber wie oben erwähnt, kann dieser Satz gelegentlich fälschlicherweise bestimmte Zusammensetzungen als Primzahl charakterisieren. Es ist wichtig, dies zu berücksichtigen und Ihre Antwort zu überprüfen, die später erklärt wird.
2. Wähle eine ganze Zahl ein zwischen 2 und n-1 (inklusive). Die genaue ganze Zahl, die Sie wählen, ist nicht wichtig. Da die Parameter für a 2 und n-1 enthalten, können Sie auch diese verwenden.
3. Berechnung ein (mod n). Die Berechnung dieses Ausdrucks erfordert einige Kenntnisse eines mathematischen Systems namens modulare Mathematik. In der modularen Mathematik kehren Zahlen bei Erreichen eines bestimmten Wertes, der als bekannt ist, auf Null zurück Modul. Das kann man sich wie eine Uhr vorstellen: Irgendwann springt der Uhrzeiger nach 12 Uhr auf 1 Uhr zurück, nicht auf 1 Uhr. Der Modul wird notiert als (mod n). In diesem Schritt rechnen Sie also mit einem Modul von n.
4. Wenn wir dies von Hand berechnen, verwenden wir den Exponenten als kurze Schreibweise. Wenn Sie keinen Taschenrechner mit Modulusfunktion haben, verwenden Sie die Exponentialschreibweise, um die Berechnung des Restes zu vereinfachen. Siehe unten:
5. Überprüfen Sie, ob ein (mod n) = ein (mod n). Wenn nicht, dann ist n zusammengesetzt. Wenn wahr, dann ist n wahrscheinlich (aber nicht sicher) eine Primzahl. Das Wiederholen des Tests mit verschiedenen Werten für a kann das Ergebnis sicherer machen, aber es gibt seltene zusammengesetzte Zahlen, die den Satz von Fermat für erfüllen alle Werte von a. Diese werden Carmichael-Zahlen genannt - die kleinste dieser Zahlen ist 561.
6. Verwenden Sie die Carmichael-Zahlen, um sich Ihres Ergebnisses sicher zu sein. Zu wissen, welche Zahlen die Carmichael-Folge erfüllen, bevor Sie fortfahren, kann Ihnen viele Kopfschmerzen ersparen, ob eine Zahl eine Primzahl ist oder nicht. Im Allgemeinen sind Carmichael-Zahlen das Produkt einzelner Primzahlen, wobei für alle Primzahlen gilt, dass wenn p ein Teiler von n ist, dann ist auch p-1 ein Teiler von n-1. Die Online-Liste der Carmichael-Zahlen kann sehr nützlich sein, um mithilfe des kleinen Satzes von Fermat zu bestimmen, ob eine Zahl eine Primzahl ist.
Methode 3 von 4: Verwenden des Miller-Rabin-Tests
Der Miller-Rabin-Test funktioniert genauso wie der kleine Satz von Fermat, behandelt aber anomale Zahlen wie Carmichael-Zahlen besser.
1. Paar n ist eine ungerade Zahl, die wir auf Primzahl testen wollen. Wie bei den oben angegebenen Methoden ist n die Variable, von der wir die Primalität von bestimmen wollen.
2. Beschäftigt n-1 aus in der Form 2 × D wodurch D ist ungerade. Die Zahl n ist prim, wenn sie ungerade ist. Also muss n - 1 gerade sein. Da n - 1 gerade ist, kann es als Zweierpotenz mal einer ungeraden Zahl geschrieben werden . Also 4 = 2 × 1; 80 = 2 × 5; und so weiter.
3. Wähle eine beliebige Zahl ein zwischen 2 und n-1. Die genaue Zahl, die Sie wählen, spielt keine Rolle - sie muss nur kleiner als n und größer als 1 . sein.
4. Berechnung ein (mod n). wenn ein = 1 oder -1 (mod n), dann hältn den Miller-Rabin-Test und ist wahrscheinlich eine Primzahl. Wie beim Kleinen Satz von Fermat kann dieser Test die Primalität einer Zahl nicht mit absoluter Sicherheit bestimmen, sondern benötigt dazu zusätzliche Tests.
5. Da das Ergebnis ungleich 1 oder -1 ist, berechneein, ein,... und so weiter, bis zu einD. Berechnen Sie a hoch d mal , bis zu 2. Wenn einer von diesen gleich 1 oder -1 ist (mod n), dann hält n der Miller-Rabin-Test und ist wahrscheinlich prim. Sobald Sie festgestellt haben, dass n den Test besteht, überprüfen Sie Ihre Antwort (siehe Schritt unten). Wenn n keinen dieser Tests besteht, ist es a zusammengesetzt Nummer.
6. wenn n erfüllt den Miller-Rabin-Test, dann wiederholen Sie dies für die anderen Werte von ein. Wenn Sie festgestellt haben, dass der Wert von n durchaus eine Primzahl sein kann, versuchen Sie es erneut mit einem anderen Zufallswert für a, um das Ergebnis des Tests zu bestätigen. Wenn n tatsächlich eine Primzahl ist, gilt dies für jeden Wert von a. Wenn n eine zusammengesetzte Zahl ist, schlägt es für drei Viertel der Werte von a . fehl. Dies gibt Ihnen mehr Sicherheit als mit dem Kleinen Satz von Fermat, bei dem bestimmte zusammengesetzte Zahlen (die Carmichael-Zahlen) den Test für jeden Wert von a . bestehen.
Methode 4 von 4: Verwenden des chinesischen Restsatzes
1. Wähle zwei Zahlen. Eine der Zahlen ist keine Primzahl und die zweite ist die Zahl, die auf Primzahl getestet wird.
- "Testnummer1" = 35
- Testnummer2 = 97
2. Wählen Sie zwei Datenpunkte größer Null und kleiner als TestNumber1, bzw. TestNumber2. Sie können nicht gleich sein.
3. Berechnen Sie den MMI (Mathematical Multiplicative Inverse) für TestNumber1 und TestNumber2
4. Erstellen Sie eine Binärtabelle für jedes MMI bis Log2 des Modulus
5. Berechnen (Data1 * TestNumber2 * MMI1 + Data2 * TestNumber1 * MMI2) % (TestNumber1 * TestNumber)
6. Überprüfen Sie, ob "Testnummer1" ist nicht prim 1
7. Prüfen Sie, ob TestNumber2 eine Primzahl ist
8. Wiederholen Sie die Schritte 1 bis 7 mindestens noch zweimal.
Tipps
- Die 168 Primzahlen unter 1000 sind: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997
- Wenn der Versuch, zu dividieren, langsamer ist als die ausgefeilteren Methoden, ist er für kleinere Zahlen immer noch effizient. Selbst beim Testen größerer Zahlen ist es nicht ungewöhnlich, zuerst die kleinen Zahlen zu überprüfen, bevor zu den fortgeschritteneren Methoden gewechselt wird.
Notwendigkeiten
- Papier, Kugelschreiber, Bleistift und/oder Taschenrechner zum Trainieren
"Prüfe, ob eine zahl eine primzahl ist"
Оцените, пожалуйста статью
