Binärzahlen lesen

Schritte
Tipps

Der Versuch, eine Reihe von Zahlen zu entziffern, die aus binären Einsen und Nullen bestehen, kann wie eine entmutigende Aufgabe erscheinen. Aber mit ein bisschen Logik kannst du herausfinden, was sie bedeuten. Die Leute haben sich daran gewöhnt, mit der Basis Zehn zu rechnen, einfach weil wir zehn Finger haben. Computer haben jedoch nur zwei „Finger“ – an und aus, oder 1 und 0. Deshalb wurde das Zahlensystem zur Basis zwei erfunden.

Schritte

Methode 1 von 3: Verwenden von Exponenten

1. Nehmen Sie eine Binärzahl, die Sie umwandeln möchten. Nehmen wir als Beispiel die folgende Zahl: 101010.

2. Multiplizieren Sie eine beliebige Binärzahl mit zwei auf den Stellenwert erhöht. Denken Sie daran, dass Ihre Binärzahlen von rechts nach links liest. Die Zahl ganz rechts ist Null.

3. Füge die Ergebnisse zusammen. Lass es uns von rechts nach links beenden.

0 × 2 = 0

1 × 2 = 2

0 × 2 = 0

1×2 = 8

0 × 2 = 0

1×2 = 32

Gesamt = 42

Methode 2 von 3: Alternative Division mit Potenzen

1. Wähle eine Binärzahl. Angenommen, wir nehmen 101. Hier verwenden Sie die gleiche Methode, jedoch etwas anders angeordnet. Möglicherweise ist dieses Setup einfacher zu verstehen.

101= (1X2) 2. Potenz + (0X2) 1. Potenz + (1X2) 0. Potenz
101= (2X2) + (0X0) + (1)
101= 4 + 0 + 1
101= 5

Die `Null` ist keine Zahl, aber der Wert dieser Stelle muss eingegeben werden.

Methode 3 von 3: Endwert

1. Finde deine Nummer. Das Beispiel, das wir verwenden werden, ist 00101010.

2. Von rechts nach links lesen. Für jeden Ort werden die Werte verdoppelt. Die erste Ziffer von rechts gesehen hat den Wert 1, die zweite eine 2, dann eine 4 usw.

3. Addiere die Werte der Einsen zusammen. Den Nullen wird die entsprechende Nummer zugewiesen, aber diese Ziffern werden nicht aufsummiert.

In diesem Beispiel addierst du also 2, 8 und 32 zusammen. Das Ergebnis ist 42.

Es gibt ein "Nein" zu 1, ein "Ja" zu 2, ein "Nein" zu 4, ein "Ja" zu 8, ein "Nein" zu 16, ein "Ja" zu 32, ein "Nein" zu 64 und ein `Nein` bei 128. "ja" bedeutet hinzufügen, "Neu" überspringt. Beim letzten kannst du aufhören.

4. Wandeln Sie den Wert in Buchstaben oder Satzzeichen um. Außerdem können Sie Zahlen von binär in dezimal oder von dezimal in binär umwandeln.

Bei Satzzeichen entspricht die 42 einem Sternchen (*). KlickenHier für einen Tisch.

Tipps

Sie können mit Binärzahlen genauso rechnen wie mit regulären Zahlen. Die Ziffer ganz rechts wird um eins erhöht, bis sie nicht mehr erhöht werden kann (in diesem Fall von 0 auf 1) und dann wird die nächste Ziffer links um eins erhöht und beginnt wieder bei Null.
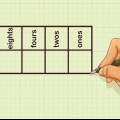
Die Zahlen, die wir heute verwenden, haben einen Stellenwert. Bei ganzen Zahlen ist die Ziffer ganz rechts eine Einheit, die nächste Ziffer eine Zehn, dann eine Hundert und so weiter. Die Stellenwerte von Binärzahlen werden in Einheiten, Paare, Vieren, Achter usw. angegeben.