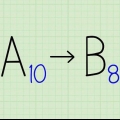Eine Binärzahl in eine Dezimalzahl umwandeln (mit Bildern)

Schritte
- Methode 1 von 2: Positionssystemmethode
- Methode 2 von 2: Verdoppelungsmethode
Tipps
Warnungen

Es binär (Basis 2) Zahlensystem hat zwei mögliche Werte, normalerweise dargestellt als 0 oder 1, für jede Position in einer Zahl. Der Unterschied zu den Dezimal (Basis 10) Zahlensystem ist, dass es für jede Position zehn mögliche Werte (0,1,2,3,4,5,6,7,8 oder 9) gibt.

Um Verwechslungen bei der Verwendung verschiedener Zahlensysteme zu vermeiden, kann die Basis einer Zahl angegeben werden, indem sie nach der Zahl tiefgestellt wird.Zum Beispiel kann die Binärzahl 10011100 zur Basis 2 geschrieben werden, indem sie als 10011100 . geschrieben wird₂.Die Dezimalzahl 156 kann als 156 . geschrieben werden₁₀ oder vollständig als "einhundertsechsundfünfzig, Basis 10".

Da das Binärsystem die Maschinensprache von Computern ist, müssen ernsthafte Programmierer vollständig verstehen, wie man Binärzahlen in Dezimalzahlen umwandelt.Die Umrechnung in umgekehrter Richtung, von dezimal in binär, ist oft zuerst schwerer zu erlernen.

Hinweis: Hier geht es NUR um Berechnungen und nicht um ASCII-Übersetzungen.

Schritte

Methode 1 von 2: Positionssystemmethode

Bildtitel Convert from Binary to Decimal Step 1

1. In diesem Beispiel verwenden wir die Binärzahl 10011011₂ in dezimal umwandeln. Zähle die Zweierpotenzen von rechts nach links auf. Beginnen Sie mit 2, dies hat den Wert "1".Multiplizieren Sie die Exponenten mit 1 für jede Potenz.Stoppen Sie, wenn die Anzahl der Elemente in der Liste der Anzahl der Stellen in der Binärzahl entspricht. Die Beispielnummer 10011011 hat 8 Stellen, die Liste sieht also so aus: 128, 64, 32, 16, 8, 4, 2, 1

Bildtitel Convert from Binary to Decimal Step 2

2. Schreiben Sie die Binärzahl unter die Liste.

Bildtitel Convert from Binary to Decimal Step 3

3. Verbinde Binärzahlen mit Zweierpotenzen. Zeichnen Sie Linien, die jede Binärziffer mit der entsprechenden zweiten Potenz darüber verbinden.Beginnen Sie mit der ersten Binärziffer von rechts und fahren Sie fort, bis Sie alle Binärziffern und die Potenzen verbunden haben.

Bildtitel Convert from Binary to Decimal Step 4

4. Gehen Sie alle Ziffern der Binärzahl durch. Wenn die Zahl eine 1 ist, schreiben Sie die entsprechende zweite Potenz unter die Linie, direkt unter die Zahl.Wenn die Zahl eine 0 ist, schreibe eine 0 unter die Linie.

Bildtitel Convert from Binary to Decimal Step 5

5. Addiere die Zahlen unter der Linie. Die Summe sollte 155 . betragen. Dies ist das dezimale Äquivalent der Binärzahl 10011011.Oder mit tiefgestellter Basis geschrieben:

Bildtitel Convert from Binary to Decimal Step 6

6. Wenn Sie diese Methode häufig wiederholen, werden Sie feststellen, dass Sie sich die Zweierpotenzen besser merken, sodass Sie Schritt 1 überspringen können.

Methode 2 von 2: Verdoppelungsmethode

1. Diese Methode verwendet keine Kräfte. Daher ist es besser geeignet, wenn Sie größere Zahlen auswendig umrechnen möchten, da Sie sich nur die Zwischensumme merken müssen.

Bildtitel Convert from Binary to Decimal Step 8

2. Beginnen Sie mit der Ziffer ganz links von der angegebenen Binärzahl. Für jede nachfolgende Zahl von links nach rechts verdoppeln Sie die vorherige Summe und addieren Sie sie zur aktuellen Zahl. Um zum Beispiel die Nummer 1011001 einzugeben₂ Um in Dezimalzahlen umzuwandeln, gehen wir wie folgt vor:

Bildtitel Convert from Binary to Decimal Step 9

3. 1011001 → 0 * 2 + 1 = 1

Bildtitel Convert from Binary to Decimal Step 10

4. 1011001 → 1 * 2 + 0 = 2

Bildtitel Convert from Binary to Decimal Step 11

5. 1011001 → 2 * 2 + 1 = 5

Bildtitel Convert from Binary to Decimal Step 12

6. 1011001 → 5 * 2 + 1 = 11

Bildtitel Convert from Binary to Decimal Step 13

7. 1011001 → 11 * 2 + 0 = 22

Bildtitel Convert from Binary to Decimal Step 14

8. 1011001 → 22 * 2 + 0 = 44

Bildtitel Convert from Binary to Decimal Step 15

9. 1011001 → 44 * 2 + 1 = 89₁₀

Bildtitel Convert from Binary to Decimal Step 16

10. Wie die Positionssystemmethode kann diese Methode modifiziert werden, um von einem beliebigen Zahlensystem in eine Dezimalzahl umzuwandeln.Verdoppelung wird hier verwendet, weil die Basis zwei ist. Wenn die angegebene Zahl eine andere Basis hat, verwenden Sie diese anstelle von 2. Wenn die Zahl beispielsweise die Basis 37 hat, vertausche *2 mit *37. Das Ergebnis ist immer eine Dezimalzahl (Basis 10). :)

Tipps

Übe viel. Versuchen Sie es mit den Binärzahlen 11010001₂, 11001₂, und 11110001₂.Ihre dezimalen Äquivalente sind 209₁₀, 25₁₀, und 241₁₀.
Der mit Microsoft Windows gelieferte Rechner kann diese Konvertierung auch für Sie durchführen, aber wenn Sie ein Programmierer sind, ist es besser, dass Sie die Funktionsweise dieser Konvertierung gut kennen. Die Optionen dieses Rechners finden Sie über die "Aussicht" Menü und dann "Wissenschaftlich" (oder "Programmierer"). Mit Linux können Sie verwenden galculator.