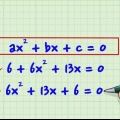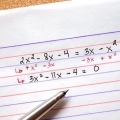Hier ist klar warum  , weil
, weil  steht im Nenner und kann nicht durch Null geteilt werden.
steht im Nenner und kann nicht durch Null geteilt werden. Bei Bedarf können Sie die linke Seite verlängern, um sicherzustellen, dass die Quadratur funktioniert. 

Jetzt können wir die Absolutwertzeichen loswerden, indem wir  rechts platzieren. Wir können dies tun, weil der Absolutwert nicht zwischen positiven und negativen Zahlen unterscheidet, also beide gültig sind. Dieses Detail ist der Grund, warum die quadratische Gleichung es ermöglicht, als Ergebnis zwei Wurzeln zu erhalten.
rechts platzieren. Wir können dies tun, weil der Absolutwert nicht zwischen positiven und negativen Zahlen unterscheidet, also beide gültig sind. Dieses Detail ist der Grund, warum die quadratische Gleichung es ermöglicht, als Ergebnis zwei Wurzeln zu erhalten. 
Vereinfachen wir diesen Ausdruck noch ein bisschen. Da die Quadratwurzel eines Quotienten der Quotient der Quadratwurzeln ist, können wir die rechte Seite schreiben als  Dann können wir die Quadratwurzel des Nenners ziehen.
Dann können wir die Quadratwurzel des Nenners ziehen. 


Quadratische teilung lernen
Eine der wichtigsten Fähigkeiten für Mathematikstudenten ist die ABC-Formel, oder 


Schritte
1. Beginnen Sie mit der Standardform einer allgemeinen quadratischen Gleichung. Obwohl jeder Vergleich mit einem Begriff wie  in, ist quadratisch, die Standardform setzt alles auf Null. Erinnere dich daran
in, ist quadratisch, die Standardform setzt alles auf Null. Erinnere dich daran  sind Koeffizienten, die jede ganze Zahl sein können, daher können Sie jetzt keine Zahlen für die Variablen eingeben - wir möchten mit der allgemeinen Form arbeiten.
sind Koeffizienten, die jede ganze Zahl sein können, daher können Sie jetzt keine Zahlen für die Variablen eingeben - wir möchten mit der allgemeinen Form arbeiten.
 in, ist quadratisch, die Standardform setzt alles auf Null. Erinnere dich daran
in, ist quadratisch, die Standardform setzt alles auf Null. Erinnere dich daran  sind Koeffizienten, die jede ganze Zahl sein können, daher können Sie jetzt keine Zahlen für die Variablen eingeben - wir möchten mit der allgemeinen Form arbeiten.
sind Koeffizienten, die jede ganze Zahl sein können, daher können Sie jetzt keine Zahlen für die Variablen eingeben - wir möchten mit der allgemeinen Form arbeiten. - Die einzige Bedingung ist, dass
, andernfalls wird die Gleichung zu einer linearen Gleichung vereinfacht. Sehen Sie nach, ob Sie allgemeine Lösungen für spezielle Fälle finden können, in denen
und
.
2. ziehen C  von beiden seiten. Unser Ziel ist es zu isolieren
von beiden seiten. Unser Ziel ist es zu isolieren  . Wir beginnen damit, dass wir einen der Koeffizienten auf die andere Seite verschieben, sodass die linke Seite nur aus Termen mit . besteht
. Wir beginnen damit, dass wir einen der Koeffizienten auf die andere Seite verschieben, sodass die linke Seite nur aus Termen mit . besteht  .
.
 von beiden seiten. Unser Ziel ist es zu isolieren
von beiden seiten. Unser Ziel ist es zu isolieren  . Wir beginnen damit, dass wir einen der Koeffizienten auf die andere Seite verschieben, sodass die linke Seite nur aus Termen mit . besteht
. Wir beginnen damit, dass wir einen der Koeffizienten auf die andere Seite verschieben, sodass die linke Seite nur aus Termen mit . besteht  .
.
3. Teilen Sie beide Seiten ein  . Beachten Sie, dass wir diese im vorherigen Schritt hätten austauschen können und immer noch die gleiche Antwort erhalten. Denken Sie daran, dass das Teilen eines Polynoms durch etwas bedeutet, dass jeder seiner einzelnen Terme geteilt wird. So lässt sich das Quadrat leichter teilen.
. Beachten Sie, dass wir diese im vorherigen Schritt hätten austauschen können und immer noch die gleiche Antwort erhalten. Denken Sie daran, dass das Teilen eines Polynoms durch etwas bedeutet, dass jeder seiner einzelnen Terme geteilt wird. So lässt sich das Quadrat leichter teilen.
 . Beachten Sie, dass wir diese im vorherigen Schritt hätten austauschen können und immer noch die gleiche Antwort erhalten. Denken Sie daran, dass das Teilen eines Polynoms durch etwas bedeutet, dass jeder seiner einzelnen Terme geteilt wird. So lässt sich das Quadrat leichter teilen.
. Beachten Sie, dass wir diese im vorherigen Schritt hätten austauschen können und immer noch die gleiche Antwort erhalten. Denken Sie daran, dass das Teilen eines Polynoms durch etwas bedeutet, dass jeder seiner einzelnen Terme geteilt wird. So lässt sich das Quadrat leichter teilen.
4.Teile das Quadrat. Denken Sie daran, dass das Ziel darin besteht, einen Ausdruck zu erstellen  umschreiben als
umschreiben als  wodurch
wodurch  ist ein Koeffizient. Das ist dir vielleicht nicht sofort klar. Um es klarer zu machen, schreibe um
ist ein Koeffizient. Das ist dir vielleicht nicht sofort klar. Um es klarer zu machen, schreibe um  wenn
wenn  indem man den Begriff mit multipliziert
indem man den Begriff mit multipliziert  Wir können dies tun, weil die Multiplikation mit 1 nichts ändert. Das können wir jetzt in unserem Fall deutlich erkennen
Wir können dies tun, weil die Multiplikation mit 1 nichts ändert. Das können wir jetzt in unserem Fall deutlich erkennen  , es fehlt also nur der Begriff
, es fehlt also nur der Begriff  . Um das Quadrat zu teilen, fügen wir es also auf beiden Seiten hinzu - nämlich,
. Um das Quadrat zu teilen, fügen wir es also auf beiden Seiten hinzu - nämlich,  Und dann können wir natürlich faktorisieren.
Und dann können wir natürlich faktorisieren.
 umschreiben als
umschreiben als  wodurch
wodurch  ist ein Koeffizient. Das ist dir vielleicht nicht sofort klar. Um es klarer zu machen, schreibe um
ist ein Koeffizient. Das ist dir vielleicht nicht sofort klar. Um es klarer zu machen, schreibe um  wenn
wenn  indem man den Begriff mit multipliziert
indem man den Begriff mit multipliziert  Wir können dies tun, weil die Multiplikation mit 1 nichts ändert. Das können wir jetzt in unserem Fall deutlich erkennen
Wir können dies tun, weil die Multiplikation mit 1 nichts ändert. Das können wir jetzt in unserem Fall deutlich erkennen  , es fehlt also nur der Begriff
, es fehlt also nur der Begriff  . Um das Quadrat zu teilen, fügen wir es also auf beiden Seiten hinzu - nämlich,
. Um das Quadrat zu teilen, fügen wir es also auf beiden Seiten hinzu - nämlich,  Und dann können wir natürlich faktorisieren.
Und dann können wir natürlich faktorisieren.
 , weil
, weil  steht im Nenner und kann nicht durch Null geteilt werden.
steht im Nenner und kann nicht durch Null geteilt werden.5. Schreibe die rechte Seite auf einen gemeinsamen Nenner. Wir wollen, dass beide Nenner sind  sind, also multipliziere den Begriff
sind, also multipliziere den Begriff  von
von  .
.
 sind, also multipliziere den Begriff
sind, also multipliziere den Begriff  von
von  .
.
6. Berechne die Quadratwurzel beider Seiten. Es ist jedoch wichtig, dass Sie verstehen, dass Sie damit im Wesentlichen zwei Schritte unternehmen. Wenn Sie die Quadratwurzel von ziehen  , dann bekommst du
, dann bekommst du  nicht. Sie erhalten im Grunde den absoluten Wert davon,
nicht. Sie erhalten im Grunde den absoluten Wert davon,  . Dieser absolute Wert ist essentiell um beide Wurzeln zu erhalten - einfaches Platzieren von Quadratwurzeln über beiden Seiten ergibt nur eine der Wurzeln.
. Dieser absolute Wert ist essentiell um beide Wurzeln zu erhalten - einfaches Platzieren von Quadratwurzeln über beiden Seiten ergibt nur eine der Wurzeln.
 , dann bekommst du
, dann bekommst du  nicht. Sie erhalten im Grunde den absoluten Wert davon,
nicht. Sie erhalten im Grunde den absoluten Wert davon,  . Dieser absolute Wert ist essentiell um beide Wurzeln zu erhalten - einfaches Platzieren von Quadratwurzeln über beiden Seiten ergibt nur eine der Wurzeln.
. Dieser absolute Wert ist essentiell um beide Wurzeln zu erhalten - einfaches Platzieren von Quadratwurzeln über beiden Seiten ergibt nur eine der Wurzeln.
 rechts platzieren. Wir können dies tun, weil der Absolutwert nicht zwischen positiven und negativen Zahlen unterscheidet, also beide gültig sind. Dieses Detail ist der Grund, warum die quadratische Gleichung es ermöglicht, als Ergebnis zwei Wurzeln zu erhalten.
rechts platzieren. Wir können dies tun, weil der Absolutwert nicht zwischen positiven und negativen Zahlen unterscheidet, also beide gültig sind. Dieses Detail ist der Grund, warum die quadratische Gleichung es ermöglicht, als Ergebnis zwei Wurzeln zu erhalten.
 Dann können wir die Quadratwurzel des Nenners ziehen.
Dann können wir die Quadratwurzel des Nenners ziehen.
7. isolieren x  durch Subtrahieren
durch Subtrahieren B 2 ein  auf beiden Seiten.
auf beiden Seiten.
 durch Subtrahieren
durch Subtrahieren  auf beiden Seiten.
auf beiden Seiten.
8. Schreibe die rechte Seite auf einen gemeinsamen Nenner. Dies ist nicht wie die abc-Formel, die Formel zum Lösen einer quadratischen Gleichung in Standardform. Das funktioniert für jeden  und gibt
und gibt  als Ergebnis, das eine reelle oder komplexe Zahl sein kann. Um zu überprüfen, ob dieser Vorgang funktioniert, führen Sie einfach die Schritte in diesem Artikel in umgekehrter Reihenfolge aus, um zum Standardformular zurückzukehren.
als Ergebnis, das eine reelle oder komplexe Zahl sein kann. Um zu überprüfen, ob dieser Vorgang funktioniert, führen Sie einfach die Schritte in diesem Artikel in umgekehrter Reihenfolge aus, um zum Standardformular zurückzukehren.
 und gibt
und gibt  als Ergebnis, das eine reelle oder komplexe Zahl sein kann. Um zu überprüfen, ob dieser Vorgang funktioniert, führen Sie einfach die Schritte in diesem Artikel in umgekehrter Reihenfolge aus, um zum Standardformular zurückzukehren.
als Ergebnis, das eine reelle oder komplexe Zahl sein kann. Um zu überprüfen, ob dieser Vorgang funktioniert, führen Sie einfach die Schritte in diesem Artikel in umgekehrter Reihenfolge aus, um zum Standardformular zurückzukehren.
Tipps
- Es ist interessant zu bemerken, dass die abc-Formel auch für komplexe Koeffizienten gilt, obwohl Sie etwas mehr vereinfachen müssen, um die endgültige Antwort zu erhalten, und die Wurzeln keine konjugierten Paare sind. Probleme mit quadratischen Ausdrücken sind jedoch fast immer mit reellen Koeffizienten gegeben.
"Quadratische teilung lernen"
Оцените, пожалуйста статью