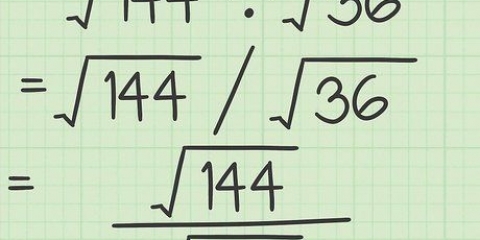Die Ableitung der Quadratwurzel von x finden

Schritte

Wenn Sie in der Schule Mathematik gemacht haben, müssen Sie die Potenzregel zur Bestimmung der Ableitung einfacher Funktionen gelernt haben. Wenn die Funktion jedoch eine Quadratwurzel oder ein Radikal enthält, wie z $\sqrt{x}$ ${sqrt{x}}$ , dann scheint die Herrschaft der Macht schwierig anzuwenden. Mit einer einfachen Substitution von Exponenten wird die Bestimmung der Ableitung einer solchen Funktion sehr einfach. Sie können dann dieselbe Substitution anwenden und die Kettenregel verwenden, um die Ableitung vieler anderer Funktionen mit Wurzeln zu finden.

Schritte

Methode 1 von 3: Anwenden der Potenzregel

Bildtitel Differentiate the Square Root of X Step 1

1. Sehen Sie sich die Potenzregel für Derivate noch einmal an. Die erste Regel, die du wahrscheinlich gelernt hast, um Ableitungen zu finden, ist die Machtregel. Diese Regel besagt, dass für eine Variable

x

$x$ hoch einer Zahl

ein

$ein$ , ist die Ableitung und wird wie folgt berechnet:

$F (x) = x ein$ ${displaystyle f(x)=x^{a}}$
$F Sex (x) = ein x^{ein - 1}$ ${displaystyle f^{prime}(x)=ax^{a-1}}$
Sehen Sie sich die folgenden Beispielfunktionen und ihre Ableitungen an:

wenn $F (x) = x 2$ ${displaystyle f(x)=x^{2}}$ , dann $F Sex (x) = 2 x$ ${displaystyle f^{prime}(x)=2x}$
wenn $F (x) = 3 x 2$ ${displaystyle f(x)=3x^{2}}$ , dann $F Sex (x) = 2 * 3 x = 6 x$ ${displaystyle f^{prime}(x)=2*3x=6x}$
wenn $F (x) = x 3$ ${displaystyle f(x)=x^{3}}$ , dann $F Sex (x) = 3 x^{2}$ ${displaystyle f^{prime}(x)=3x^{2}}$
wenn $F (x) = \frac{1}{2} x^{4}$ ${displaystyle f(x)={frac {1}{2}}x^{4}}$ , dann $F Sex (x) = 4 * \frac{1}{2} x^{3} = 2 x^{3}$ ${displaystyle f^{prime}(x)=4*{frac {1}{2}}x^{3}=2x^{3}}$

Bildtitel Differentiate the Square Root of X Step 2

2. Schreibe die Quadratwurzel als Exponenten um. Um die Ableitung einer Quadratwurzelfunktion zu bestimmen, denken Sie daran, dass die Quadratwurzel einer Zahl oder Variable auch als Exponent geschrieben werden kann. Der Term unter dem Radikal wird als Basis geschrieben und mit 1/2 . potenziert. Der Begriff wird auch als Exponent der Quadratwurzel verwendet. Sehen Sie sich die folgenden Beispiele an:

\sqrt{x} = x^{\frac{1}{2}}

${displaystyle {sqrt {x}}=x^{frac {1}{2}}}$

\sqrt{4} = 4^{\frac{1}{2}}

${displaystyle {sqrt {4}}=4^{frac {1}{2}}}$

\sqrt{3 x} = (3 x)^{\frac{1}{2}}

${displaystyle {sqrt {3x}}=(3x)^{frac {1}{2}}}$

Bildtitel Differentiate the Square Root of X Step 3

3. Wende die Machtregel an. Wenn die Funktion die einfachste Quadratwurzel ist,

F (x) = \sqrt{x}

${displaystyle f(x)={sqrt {x}}}$ , Dann wenden Sie die Potenzregel wie folgt an, um die Ableitung zu finden:

F (x) = \sqrt{x}

${displaystyle f(x)={sqrt {x}} }$ (Schreiben Sie die ursprüngliche Funktion auf.)

F (x) = x (\frac{1}{2})

${displaystyle f(x)=x^{({frac {1}{2}})} }$ (Schreibe die Wurzel in einen Exponenten um.)

F Sex (x) = \frac{1}{2} x^{(\frac{1}{2} - 1)}

${displaystyle f^{prime}(x)={frac {1}{2}}x^{({frac {1}{2}}-1)} }$ (Finden Sie die Ableitung mit der Potenzregel.)

F Sex (x) = \frac{1}{2} x^{(- \frac{1}{2})}

${displaystyle f^{prime}(x)={frac {1}{2}}x^{(-{frac {1}{2}})} }$ (Vereinfachen Sie den Exponenten.)

Bildtitel Differentiate the Square Root of X Step 4

4. Vereinfachen Sie das Ergebnis. Zu diesem Zeitpunkt sollten Sie wissen, dass ein negativer Exponent bedeutet, dass Sie die Umkehrung der Zahl mit dem positiven Exponenten nehmen. Der Exponent von

- \frac{1}{2}

${displaystyle -{frac {1}{2}}}$ bedeutet, dass die Quadratwurzel der Basis zum Nenner eines Bruchs wird.

Weiter mit der Quadratwurzel der Funktion x von oben lässt sich die Ableitung wie folgt vereinfachen:

F Sex (x) = \frac{1}{2} x^{- \frac{1}{2}}

${displaystyle f^{prime}(x)={frac {1}{2}}x^{-{frac {1}{2}}}}$

F Sex (x) = \frac{1}{2} * \frac{1}{\sqrt{x}}

${displaystyle f^{prime}(x)={frac {1}{2}}*{frac {1}{sqrt {x}}}}$

F Sex (x) = 12 \sqrt{x}

${displaystyle f^{prime}(x)={frac {1}{2{sqrt {x}}}}}}$

Methode 2 von 3: Anwenden der Kettenregel für Quadratwurzelfunktionen

Bildtitel Differentiate the Square Root of X Step 5

1. Überarbeitung der Kettenregel für Funktionen. Die Kettenregel ist eine Regel für Ableitungen, die Sie verwenden, wenn die ursprüngliche Funktion eine Funktion innerhalb einer anderen Funktion kombiniert. Die Kettenregel besagt, dass für zwei Funktionen

F (x)

$f(x)$ und

g (x)

${displaystyle g(x)}$ , die Ableitung der Kombination der beiden Funktionen ergibt sich wie folgt:

wenn $ja = F (g (x))$ ${displaystyle y=f(g(x))}$ , dann $ja Sex = F^{Sex} (g) * g^{Sex} (x)$ ${displaystyle y^{prime}=f^{prime}(g)*g^{prime}(x)}$ .

Bildtitel Differentiate the Square Root of X Step 6

2. Definieren Sie die Kettenregelfunktionen. Wenn Sie die Kettenregel verwenden, müssen Sie zuerst die beiden Funktionen definieren, aus denen Ihre kombinierte Funktion besteht. Bei Quadratwurzelfunktionen ist die äußerste Funktion

F (g)

${displaystyle f(g)}$ die Quadratwurzelfunktion und die innerste Funktion

g (x)

${displaystyle g(x)}$ die Funktion unter dem Radikal.

Beispiel: Angenommen, Sie haben die Ableitung von

\sqrt{3 x + 2}

${displaystyle {sqrt {3x+2}}}$ etwas finden wollen. Definieren Sie dann die beiden Teile wie folgt:

F (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

g (x) = (3 x + 2)

${displaystyle g(x)=(3x+2)}$

Bildtitel Differentiate the Square Root of X Step 7

3. Finden Sie die Ableitungen der beiden Funktionen. Um die Kettenregel auf die Quadratwurzel einer Funktion anzuwenden, müssen Sie zunächst die Ableitung der allgemeinen Quadratwurzelfunktion ermitteln:

F (g) = \sqrt{g} = g^{\frac{1}{2}}

${displaystyle f(g)={sqrt {g}}=g^{frac {1}{2}}}$

F Sex (g) = \frac{1}{2} g^{- \frac{1}{2}}

${displaystyle f^{prime}(g)={frac {1}{2}}g^{-{frac {1}{2}}}}$

F Sex (g) = 12 \sqrt{g}

${displaystyle f^{prime}(g)={frac {1}{2{sqrt {g}}}}}}$

Bestimmen Sie dann die Ableitung der zweiten Funktion:

g (x) = (3 x + 2)

${displaystyle g(x)=(3x+2)}$

g Sex (x) = 3

${displaystyle g^{prime}(x)=3}$

Bildtitel Differentiate the Square Root of X Step 8

4. Kombinieren Sie die Funktionen in der Kettenregel. Die Kettenregel lautet

ja Sex = F^{Sex} (g) * g^{Sex} (x)

${displaystyle y^{prime}=f^{prime}(g)*g^{prime}(x)}$ . Kombinieren Sie die Ableitungen wie folgt:

ja Sex = 12 \sqrt{g} * 3

${displaystyle y^{prime}={frac {1}{2{sqrt {g}}}}*3}$

ja Sex = 12 \sqrt{(3 x + 2} * 3

${displaystyle y^{prime}={frac {1}{2{sqrt {(3x+2}}}}*3}$

ja Sex = 32 \sqrt{(3 x + 2}

${displaystyle y^{prime}={frac {3}{2{sqrt {(3x+2}}}}}}$

Methode 3 von 3: Schnelles Finden der Ableitungen von Wurzelfunktionen

Bildtitel Differentiate the Square Root of X Step 9

1. Bestimmen Sie Ableitungen einer Quadratwurzelfunktion mit einer schnellen Methode. Wenn Sie die Ableitung der Quadratwurzel einer Variablen oder Funktion ermitteln möchten, können Sie eine einfache Regel anwenden: Die Ableitung ist immer die Ableitung der Zahl unter dem Radikal, dividiert durch das Doppelte der ursprünglichen Quadratwurzel. Symbolisch kann dies dargestellt werden als:

wenn $F (x) = \sqrt{Sie}$ ${displaystyle f(x)={sqrt {u}}}$ , dann $F Sex (x) = Sie Sex 2 \sqrt{Sie}$ ${displaystyle f^{prime}(x)={frac {u^{prime}}{2{sqrt {u}}}}}$

Bildtitel Differentiate the Square Root of X Step 10

2. Finden Sie die Ableitung der Zahl unter dem Radikal. Dies ist eine Zahl oder Funktion unter dem Quadratwurzelzeichen. Um diese schnelle Methode zu verwenden, finden Sie einfach die Ableitung der Zahl unter dem Radikal. Schauen Sie sich die folgenden Beispiele an:

In der Funktion

\sqrt{5 x + 2}

${displaystyle {sqrt {5x+2}}}$ , ist die Wurzelzahl

(5 x + 2)

${displaystyle (5x+2)}$ . Die Ableitung ist

5

$5$ .

In der Funktion

\sqrt{3 x} 4

${displaystyle {sqrt {3x^{4}}}}$ , ist die Wurzelzahl

3 x 4

${displaystyle 3x^{4}}$ . Die Ableitung ist

12 x 3

${displaystyle 12x^{3}}$ .

In der Funktion

\sqrt{S ich n (x)}

${displaystyle {sqrt {sin(x)}}}$ , ist die Wurzelzahl

Sünde (x)

${displaystylesin(x)}$ . Die Ableitung ist

weil (x)

${displaystyle cos(x)}$ .

Bildtitel Differentiate the Square Root of X Step 11

3. Schreibe die Ableitung der Wurzelzahl als Zähler eines Bruchs. Die Ableitung einer Quadratwurzelfunktion enthält einen Bruch. Der Zähler dieses Bruchs ist die Ableitung der Wurzelzahl. In den obigen Beispielfunktionen sieht der erste Teil der Ableitung also so aus:

wenn

F (x) = \sqrt{5 x + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , dann

F Sex (x) = \frac{5}{Nenner}

${displaystyle f^{prime}(x)={frac {5}{text{Nenner}}}}$

wenn

F (x) = \sqrt{3 x} 4

${displaystyle f(x)={sqrt {3x^{4}}}}}$ , dann

F Sex (x) = 12 x 3 Nenner

${displaystyle f^{prime}(x)={frac {12x^{3}}{text{Nenner}}}}$

wenn

F (x) = \sqrt{Sünde (x)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , dann

F Sex (x) = weil (x) Nenner

${displaystyle f^{prime}(x)={frac {cos(x)}{text{Nenner}}}}$

Bildtitel Differentiate the Square Root of X Step 12

4. Schreiben Sie den Nenner als das Doppelte der ursprünglichen Quadratwurzel. Bei dieser schnellen Methode ist der Nenner das Doppelte der ursprünglichen Quadratwurzelfunktion. In den drei obigen Beispielfunktionen sind die Nenner der Ableitungen also:

wenn

F (x) = \sqrt{5 x + 2}

${displaystyle f(x)={sqrt {5x+2}}}$ , dann

F Sex (x) = Zähler 2 \sqrt{5 x + 2}

${displaystyle f^{prime}(x)={frac {text{counter}}{2{sqrt {5x+2}}}}}$

wenn

F (x) = \sqrt{3 x} 4

${displaystyle f(x)={sqrt {3x^{4}}}}}$ , dann

F Sex (x) = Zähler 2 \sqrt{3 x} 4

${displaystyle f^{prime}(x)={frac {text{counter}}{2{sqrt {3x^{4}}}}}}}$

wenn

F (x) = \sqrt{Sünde (x)}

${displaystyle f(x)={sqrt {sin(x)}}}$ , dann

F Sex (x) = Zähler 2 \sqrt{Sünde (x)}

${displaystyle f^{prime}(x)={frac {text{counter}}{2{sqrt {sin(x)}}}}}$

Bildtitel Differentiate the Square Root of X Step 13

5. Kombiniere Zähler und Nenner, um die Ableitung zu finden. Füge die beiden Hälften des Bruchs zusammen und das Ergebnis ist die Ableitung der ursprünglichen Funktion.

wenn