Die Formel zur Berechnung der Länge des Apothems lautet wie folgt: die Seitenlänge (S) geteilt durch das 2-fache der Tangente (tan) von 180 Grad, geteilt durch die Anzahl der Seiten (n). 

Der Umfang beträgt 6 x 10 (n x S) ist gleich 60 (also P = 60). Das Apothem wird berechnet, indem man 6 und 10 für die n und S der Formel. Das Ergebnis von 2tan(180/6) ist 1,1547, und dann teilen wir 10 durch 1,1547 - das entspricht 8,66. Die Fläche des Polygons beträgt ein = ein x P / 2 oder 8,66 multipliziert mit 60 geteilt durch 2. Die Lösung ist eine Fläche von 259,8. Beachten Sie, dass die keine Klammern enthalten "Oberfläche"-Gleichung, so dass 8,66 geteilt durch 2 multipliziert mit 60 das gleiche Ergebnis ergibt, genau wie 60 geteilt durch 2 multipliziert mit 8,66. 


Den bereich regelmäßiger polygone finden
Ein regelmäßiges Vieleck ist eine zweidimensionale konvexe Figur mit kongruenten Seiten und gleichen Winkeln. Für viele Polygone, wie z Vierecke oder Dreiecke Es gibt einfache Formeln zum Ermitteln ihrer Fläche, aber wenn Sie es mit einem Polygon zu tun haben, ist es wahrscheinlich am besten, eine Formel zu wählen, die das Apothem und den Umfang der Form verwendet. Mit etwas Aufwand findet man in wenigen Minuten die Fläche der regelmäßigen Polygone.
Schritte
Teil 1 von 2: Berechnung des Umfangs

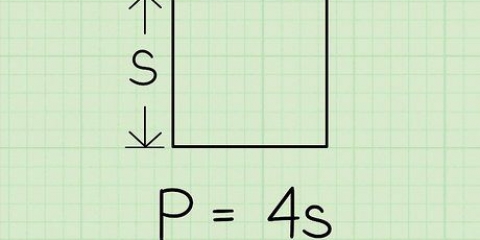
1. Berechne den Umfang. Der Umfang ist die kombinierte Länge des Umfangs einer zweidimensionalen Figur. Für ein regelmäßiges Vieleck kann dies berechnet werden, indem die Länge einer Seite mit der Anzahl der Seiten multipliziert wird (n) der Figur.

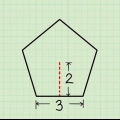
2. Bestimme das Apothem. Das Apothem eines regelmäßigen Vielecks ist die kürzeste Entfernung von seiner Mitte zu beiden Seiten, wodurch ein rechter Winkel entsteht. Das ist etwas schwieriger zu bestimmen als der Umfang.

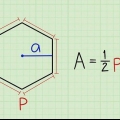
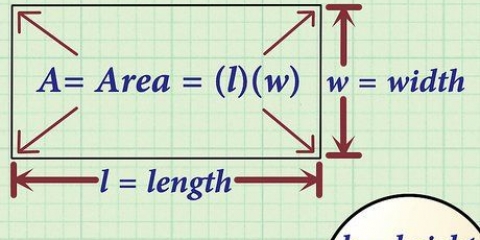
3. Kenne die richtige Formel. Die Fläche eines regelmäßigen Vielecks wird durch die Formel angegeben:Fläche = (ein x P)/2,wodurch ein ist die Länge des Apothems, und P der Umfang des Polygons.

4. Geben Sie die Werte von einein und P in der Formel zur Berechnung des Umfangs. Nehmen wir als Beispiel ein Sechseck (6 Seiten) mit der Länge 10 für jede Seite (S).
Teil 2 von 2: Die Konzepte anders verstehen

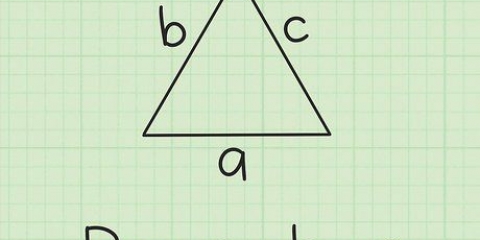
1. Ein regelmäßiges Vieleck kann als eine Ansammlung von Dreiecken betrachtet werden. Jede Seite stellt die Basis eines Dreiecks dar, und das Polygon enthält so viele Dreiecke wie Seiten. Jedes der Dreiecke ist in Grundfläche, Höhe und Fläche gleich.

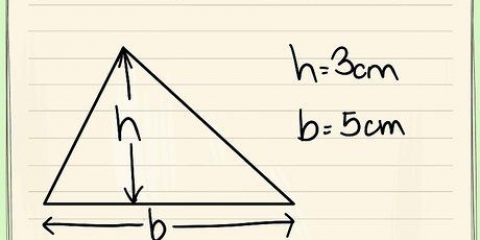
2. Verwenden Sie die Formel für die Fläche eines Dreiecks. Die Fläche eines Dreiecks beträgt 1/2 der Länge seiner Basis (die einer Seite eines Polygons entspricht), multipliziert mit seiner Höhe (die dem Apothem eines regelmäßigen Polygons entspricht).

3. Beachten Sie die Ähnlichkeiten. Auch hier ist die Formel für ein regelmäßiges Polygon 1/2 mal das Apothem multipliziert mit dem Umfang. Der Umfang ist die Länge einer Seite multipliziert mit der Anzahl der Seiten (n); bei einem regelmäßigen Vieleck repräsentiert n auch die Anzahl der Dreiecke, aus denen die Figur besteht. Die Formel ist also nichts anderes als die Fläche eines Dreiecks multipliziert mit der Anzahl der Dreiecke im Polygon.
Tipps
- Siehe wikiHow für weitere Informationen zum Arbeiten mit Quadratwurzeln und Würfelwurzeln.
- Wenn die Zeichnung Ihres Achtecks (oder einer anderen Form) in Dreiecke unterteilt ist und die Fläche eines Dreiecks beschriftet ist, benötigen Sie das Apothem nicht mehr. Nehmen Sie einfach die Fläche dieses einen Dreiecks und multiplizieren Sie sie mit der Anzahl der Seiten im ursprünglichen Polygon.
"Den bereich regelmäßiger polygone finden"
Оцените, пожалуйста статью