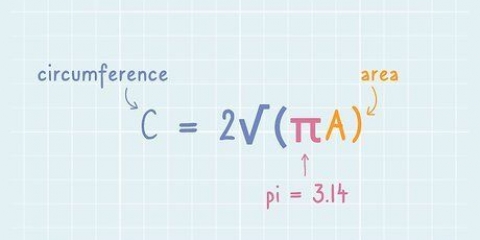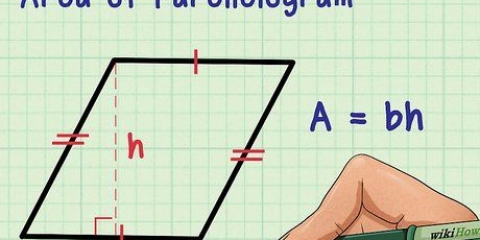Für kleine Formen können Sie Zentimeter verwenden, während Meter oder Kilometer für größere Umfänge besser geeignet sind. Wenn die gegenüberliegenden Seiten von Rechtecken gleich sind, müssen Sie nur eine der gegenüberliegenden Seiten messen. 
Fahren Sie mit dem Beispiel fort: Stellen Sie sich vor, dass die Breite Ihres Rechtecks zusätzlich zu einer Länge von 3 cm 5 cm beträgt. 

In diesem Beispiel berechnen Sie also 3 + 3 + 5 + 5 = 16 (den Umfang). Für Rechtecke kann man auch die Formel 2 x (Länge + Breite) verwenden, da Länge und Breite der gegenüberliegenden Seiten gleich sind und sich damit verdoppeln. In unserem Beispiel ist dies also: 2 x 8 = 16. 
Quadrat: Länge jeder Seite x 4 Dreieck: alle Seiten zusammenzählen Unregelmäßiges Polygon: Addiere alle Seiten zusammen Kreis: 2 x π x Radius oder π x Durchmesser. Das π-Symbol steht für Pi (ausgesprochen pie). Wenn Sie eine π-Taste auf Ihrem Taschenrechner haben, können Sie diese verwenden, um diese Formel genauer zu verwenden. Wenn nicht, können Sie den Wert von π auf 3,14 . runden. Der Begriff "Radius" bezieht sich auf den Abstand zwischen dem Mittelpunkt eines Kreises und seiner äußeren Begrenzung (Umfang), während sich "Durchmesser" auf die Länge einer imaginären Linie zwischen zwei gegenüberliegenden Punkten auf dem Umfang eines Kreises bezieht, die durch den Mittelpunkt von der kreis, der kreis geht. 

Sie können die Form in vertikale und horizontale Segmente einer Einheit (cm, m) unterteilen, wenn Sie visualisieren möchten, wie die Flächenmessung aussehen wird. 
Sie können `Quadrateinheiten/Quadrateinheiten` schreiben als: cm² m² km² 
Parallelogramm: Basis x Höhe Quadrat: Seite 1 x Seite 2 Dreieck: ½ x Basis x Höhe. Einige Mathematiker verwenden die Notation: A=½bh. Kreis: π x r² (wobei r = Radius) Der Begriff "Radius" bezieht sich auf den Abstand zwischen dem Mittelpunkt eines Kreises und seiner äußeren Grenze (Umfang), und die kleine zwei hochgestellt (das Quadrat) zeigt an, dass der Wert, zu dem die beiden gehören, mit sich selbst multipliziert wird.
Fläche und umfang bestimmen
Der Umfang ist die Länge der gesamten äußeren Begrenzung einer ebenen (zweidimensionalen) Figur, und die Fläche ist das Maß für ihre Größe. Fläche und Umfang sind äußerst nützliche Messungen, die bei Haushaltsprojekten, Bauarbeiten, Heimwerkerprojekten und bei der Schätzung der benötigten Materialmenge verwendet werden können. Wenn Sie beispielsweise einen Raum streichen möchten, müssen Sie wissen, wie viel Farbe Sie benötigen, also wie viel Oberfläche die Farbe kann bedecken. Dasselbe kann man sagen, wenn man einen Garten anlegt, einen Zaun baut oder verschiedene andere Hausarbeiten erledigt. In diesen Situationen können Sie Fläche und Umfang nutzen, um beim Materialeinkauf Zeit und Geld zu sparen.
Schritte
Teil 1 von 2: Umfang bestimmen

1. Bestimmen Sie die Form, die Sie messen möchten. Der Umfang ist die äußere Grenze um eine geschlossene geometrische Figur, und unterschiedliche Formen erfordern unterschiedliche Ansätze. Wenn die Form, deren Umfang Sie suchen möchten, keine geschlossene Form ist, kann der Umfang nicht bestimmt werden.
- Wenn Sie zum ersten Mal den Umfang berechnen, versuchen Sie es mit einem Rechteck oder einem Quadrat. Diese regelmäßigen Formen erleichtern die Bestimmung des Umfangs.

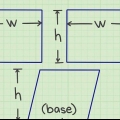
2. Zeichnen Sie ein Rechteck auf ein Blatt Papier. Sie verwenden dieses Rechteck als Übungsform und bestimmen seinen Umfang. Stellen Sie sicher, dass die gegenüberliegenden Seiten Ihres Rechtecks die gleiche Länge haben.

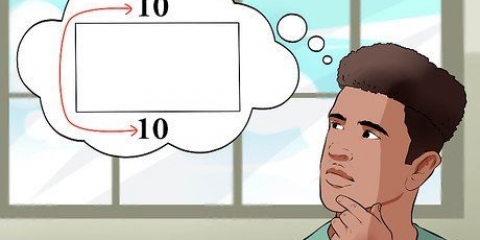
3. Bestimmen Sie die Länge einer Seite Ihres Rechtecks. Sie können dies mit einem Lineal, Maßband oder mit Ihrem eigenen Beispiel tun. Schreibe diese Zahl neben die Seite, die sie repräsentiert, damit du die Länge nicht vergisst. Angenommen, die Länge einer Seite Ihres Rechtecks beträgt 3 cm.

4. Bestimmen Sie die Breite einer Seite Ihres Rechtecks. Sie können die Breite mit einem Lineal, Maßband oder einem eigenen Beispiel messen. Schreiben Sie den Wert für Ihre Breite neben die horizontale Seite Ihres Rechtecks, das es darstellt.

5. Schreiben Sie die richtigen Maße auf die gegenüberliegenden Seiten Ihres Rechtecks. Rechtecke haben vier Seiten, aber die Länge der gegenüberliegenden Seiten ist gleich. Dies gilt auch für die Breite Ihres Rechtecks. Schreiben Sie die im Beispiel verwendete Länge und Breite (3 bzw. 5 cm) auf die gegenüberliegenden Seiten Ihres Rechtecks.

6. Füge alle Seiten zusammen. Schreiben Sie unter das Beispiel, das Sie erstellt oder aufgeschrieben haben, Folgendes: Länge + Länge + Breite + Breite.

7. Passen Sie Ihren Ansatz für verschiedene Formen an. Leider erfordern unterschiedliche Formen unterschiedliche Formeln für den Umfang. In realen Beispielen können Sie die äußere Begrenzung jeder geschlossenen geometrischen Form messen, um ihren Umfang zu bestimmen. Sie können jedoch auch die folgenden Formeln verwenden, um den Umfang anderer gängiger Formen zu ermitteln:
Teil2 von 2: Bereich bestimmen

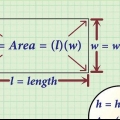
1. Bestimmen Sie die Abmessungen Ihrer Form. Zeichnen Sie ein Rechteck oder verwenden Sie dasselbe Rechteck, das Sie beim Bestimmen des Umfangs gezeichnet haben. In diesem Beispiel berechnen Sie die Fläche eines Rechtecks anhand seiner Höhe und Breite.
- Sie können mit einem Lineal oder Maßband arbeiten oder sich Ihr eigenes Beispiel einfallen lassen. In diesem Beispiel sind Länge und Breite gleich dem vorherigen Beispiel, das zum Ermitteln des Umfangs verwendet wurde: 3 bzw. 5.

2. Verstehen Sie die wahre Bedeutung der Oberfläche. Die Bestimmung der Fläche innerhalb eines Umfangs ist so, als würde man diesen leeren Raum innerhalb Ihrer Form in 1 x 1 Quadrate aufteilen. Die Fläche kann je nach Form kleiner oder größer als der Umfang sein.

3. Multiplizieren Sie die Länge Ihres Rechtecks mit der Breite. Im Beispiel: Fläche = 3 x 5, also 15 Quadratmeter. Die Maßeinheit für die Fläche sollte immer in Quadrateinheiten (Quadratkilometer, Quadratmeter usw.).).

4. Ändere deine Formel je nach Form. Leider erfordern unterschiedliche geometrische Formen einen anderen Ansatz zur Berechnung der Fläche. Sie können die folgenden Formeln verwenden, um die Fläche einiger gängiger Formen zu ermitteln:
Tipps
- Diese Flächen- und Umfangsformeln funktionieren nur für die Fläche (das Volumen) einer flachen Form. Wenn Sie den Inhalt einer dreidimensionalen Form (das Volumen) finden müssen, müssen Sie nach Formeln für das Volumen suchen, z. B. für Kegel, Würfel, Zylinder, Prismen und Pyramiden.
Notwendigkeiten
- Papier
- Bleistift
- Rechner (optional)
- Maßband (optional)
- Lineal (optional)
Оцените, пожалуйста статью