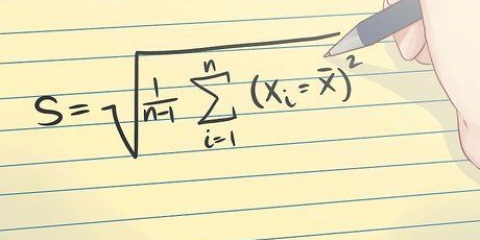Quadratsumme berechnen (sse)

Schritte

Die Quadratsumme oder SSE ist eine vorläufige statistische Berechnung, die zu unterschiedlichen Datenwerten führt. Wenn Sie über eine Reihe von Datenwerten verfügen, ist es nützlich, feststellen zu können, wie eng diese Werte miteinander verbunden sind. Sie müssen Ihre Daten in einer Tabelle organisieren und dann einige ziemlich einfache Berechnungen durchführen. Sobald Sie die SSE für einen Datensatz gefunden haben, können Sie die Varianz und Standardabweichung ermitteln.

Schritte

Methode 1 von 3: Berechnen Sie die SSE von Hand

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 1

1. Erstelle eine Tabelle mit drei Spalten. Der einfachste Weg, die SSE zu berechnen, besteht darin, mit einer Tabelle mit drei Spalten zu beginnen. Beschriften Sie die drei Spalten

Bei dem die

${displaystyle {text{Wert}}}$ ,

Abweichung

${displaystyle {text{Abweichung}}}$ , und

Abweichung 2

${displaystyle {text{Abweichung}}^{2}}$ .

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 2

2. Füllen Sie die Details aus. Die erste Spalte enthält die Werte Ihrer Messungen. Füllen Sie die Spalte aus

Bei dem die

${displaystyle {text{Wert}}}$ mit deinen Lesungen. Dies können die Ergebnisse eines Experiments, einer statistischen Studie oder einfach nur Daten aus einer mathematischen Aufgabe sein.

Angenommen, Sie arbeiten in diesem Fall mit medizinischen Daten und haben eine Liste mit den Körpertemperaturen von zehn Patienten. Die erwartete normale Körpertemperatur beträgt 98,6 Grad. Die Temperatur von zehn Patienten wird gemessen und ergibt die Werte 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 und 99,1. Die Temperatur von zehn Patienten wird gemessen und ergibt die Werte 99,0, 98,6, 98,5, 101,1, 98,3, 98,6, 97,9, 98,4, 99,2 und 99,1. Schreiben Sie diese Werte in die erste Spalte.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 3

3. Berechnen Sie den Durchschnitt. Bevor Sie den Fehler für jede Messung berechnen können, müssen Sie den Mittelwert des gesamten Datensatzes berechnen.

Der Mittelwert eines Datensatzes ist die Summe seiner Werte dividiert durch die Anzahl der Werte im Satz. Dies lässt sich symbolisch darstellen, mit der Variablen

μ

$mu$ :

μ = Σ x n

${displaystyle mu ={frac {Sigma x}{n}}}$

Für diese Daten wird der Durchschnitt wie folgt berechnet:

μ = 99, 0 + 98, 6 + 98, 5 + 101, 1 + 98, 3 + 98, 6 + 97, 9 + 98, 4 + 99, 2 + 99, 1 10

${displaystyle mu ={frac {99,0+98,6+98,5+101,1+98,3+98,6+97,9+98,4+99,2+99.1} {10}}}$

μ = 988, 7 10

${displaystyle mu ={frac {988.7}{10}}}$

μ = 98, 87

${displaystyle mu =98,87}$

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 4

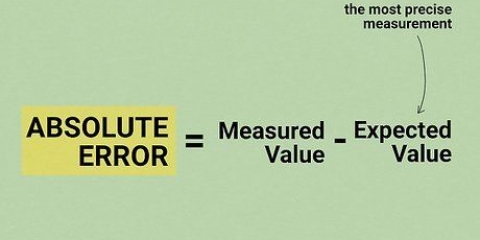
4. Berechnen Sie die einzelnen Fehlerwerte. In der zweiten Spalte deiner Tabelle musst du für jeden Datenwert die Fehlerwerte eintragen. Der Fehler ist die Differenz zwischen dem Messwert und dem Mittelwert.

Ziehen Sie für den gegebenen Datensatz den Mittelwert 98,87 von jedem gemessenen Wert ab und füllen Sie die zweite Spalte mit den Ergebnissen aus. Diese zehn Berechnungen gehen so:

99, 0 - 98, 87 = 0, 13

${displaystyle 99,0-98,87=0,13}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98,6-98,87=-0,27}$

98, 5 - 98, 87 = - 0, 37

${displaystyle 98.5-98.87=-0.37}$

101, 1 - 98, 87 = 2, 23

${displaystyle 101,1-98,87=2,23}$

98, 3 - 98, 87 = - 0, 57

${displaystyle 98,3-98,87=-0,57}$

98, 6 - 98, 87 = - 0, 27

${displaystyle 98,6-98,87=-0,27}$

97, 9 - 98, 87 = - 0, 97

${displaystyle 97,9-98,87=-0,97}$

98, 4 - 98, 87 = - 0, 47

${displaystyle 98,4-98,87=-0,47}$

99, 2 - 98, 87 = 0, 33

${displaystyle 99,2-98,87=0,33}$

99, 1 - 98, 87 = 0, 23

${displaystyle 99,1-98,87=0,23}$

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 5

5. Berechnen Sie die SSE. Suchen Sie in der dritten Spalte der Tabelle das Quadrat jedes der resultierenden Werte in der mittleren Spalte. Diese stellen die Quadrate der Abweichung vom Mittelwert für jeden gemessenen Datenwert dar.

Berechnen Sie für jeden Wert in der mittleren Spalte mit einem Taschenrechner das Quadrat. Tragen Sie die Ergebnisse wie folgt in die dritte Spalte ein:

0, 13 2 = 0, 0169

${displaystyle 0.13^{2}=0.0169}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0.27)^{2}=0.0729}$

(- 0, 37) 2 = 0, 1369

${displaystyle (-0.37)^{2}=0.1369}$

2, 23 2 = 4, 9729

${displaystyle 2.23^{2}=4.9729}$

(- 0, 57) 2 = 0, 3249

${displaystyle (-0.57)^{2}=0.3249}$

(- 0, 27) 2 = 0, 0729

${displaystyle (-0.27)^{2}=0.0729}$

(- 0, 97) 2 = 0, 9409

${displaystyle (-0.97)^{2}=0.9409}$

(- 0, 47) 2 = 0, 2209

${displaystyle (-0.47)^{2}=0.2209}$

0, 33 2 = 0, 1089

${displaystyle 0,33^{2}=0,1089}$

0, 23 2 = 0, 0529

${displaystyle 0,23^{2}=0,0529}$

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 6

6. Addiere die Quadrate der Fehler zusammen. Der letzte Schritt besteht darin, die Summe der Werte in der dritten Spalte zu finden. Das gewünschte Ergebnis ist die SSE oder die Summe der Quadrate der Fehler.

Für diesen Datensatz wird die SSE berechnet, indem die zehn Werte in der dritten Spalte addiert werden:

S S E = 6, 921

${displaystyle SSE=6.921}$

Methode 2 von 3: Erstellen Sie eine Excel-Tabelle, um die SSE zu berechnen

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 7

1. Beschriften Sie die Spalten der Tabelle. Sie erstellen eine Tabelle mit drei Spalten in Excel mit denselben drei Überschriften wie oben.

Geben Sie in Zelle A1 `Wert` als Überschrift ein.
Geben Sie in Feld B1 als Überschrift `Abweichung` ein.
Geben Sie in Feld C1 "Abweichung im Quadrat" als Überschrift ein.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 8

2. Geben Sie ihre Details ein. In der ersten Spalte müssen Sie die Werte Ihrer Messungen eingeben. Wenn das Set klein ist, können Sie es einfach von Hand eingeben. Wenn Sie einen großen Datensatz haben, müssen Sie die Daten möglicherweise kopieren und in die Spalte einfügen.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 9

3. Bestimmen Sie den Durchschnitt der Datenpunkte. Excel hat eine Funktion, die den Durchschnitt für Sie berechnet. Geben Sie in eine leere Zelle unter Ihrer Datentabelle (egal welche Zelle Sie auswählen) ein:

=Durchschnitt(A2:___)

Geben Sie kein Leerzeichen ein. Füllen Sie dieses Feld mit dem Zellennamen Ihres letzten Datenpunkts aus. Wenn Sie beispielsweise 100 Datenpunkte haben, verwenden Sie die Funktion:

=Durchschnitt(A2:A101)

Diese Funktion enthält die Daten der Zellen A2 bis A101, da die oberste Zeile die Spaltenüberschriften enthält.

Wenn Sie die Eingabetaste drücken oder auf eine andere Zelle in der Tabelle klicken, wird die neu programmierte Zelle automatisch mit dem Durchschnitt Ihrer Datenwerte gefüllt.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 10

4. Geben Sie die Fehlermessfunktion ein. In die erste leere Zelle in der Spalte `Abweichung` müssen Sie eine Funktion eingeben, um die Differenz zwischen jedem Datenpunkt und dem Mittelwert zu berechnen. Verwenden Sie dazu den Zellennamen, in dem sich der Mittelwert befindet. Nehmen wir an, Sie verwenden derzeit Zelle A104.

Die Fehlerberechnungsfunktion, die Sie in Zelle B2 eingeben, lautet:

=A2-$104$. Die Dollarzeichen werden benötigt, um sicherzustellen, dass Sie das Feld A104 für jede Berechnung sperren.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 11

5. Füllen Sie die Funktion für die quadrierten Fehler aus. In der dritten Spalte können Sie Excel anweisen, das gewünschte Quadrat zu berechnen.

Geben Sie in Zelle C2 die folgende Funktion ein:

=B2^2

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 12

6. Kopieren Sie die Funktionen, um die gesamte Tabelle zu füllen. Nachdem Sie die Funktionen in die oberste Zelle jeder Spalte, B2 bzw. C2, eingegeben haben, müssen Sie die gesamte Tabelle ausfüllen. Sie könnten die Funktion in jeder Zeile der Tabelle erneut eingeben, aber das würde viel zu lange dauern. Markieren Sie mit der Maus die Zellen B2 und C2 zusammen und ziehen Sie, ohne die Maustaste loszulassen, in die unterste Zelle jeder Spalte.

Angenommen, Sie haben 100 Datenpunkte in Ihrer Tabelle, ziehen Sie Ihre Maus zu den Zellen B101 und C101.

Wenn Sie die Maustaste loslassen, werden die Formeln in alle Zellen der Tabelle kopiert. Die Tabelle sollte automatisch mit den berechneten Werten gefüllt werden.

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 13

7. Finden Sie die SSE. Spalte C Ihrer Tabelle enthält alle quadrierten Fehlerwerte. Der letzte Schritt besteht darin, Excel die Summe dieser Werte berechnen zu lassen.

Geben Sie in einer Zelle unterhalb der Tabelle, in diesem Beispiel wahrscheinlich C102, die folgende Funktion ein:

=Summe(C2:C101)

Wenn Sie auf Enter klicken oder in einer anderen Zelle der Tabelle wegklicken, erhalten Sie den SSE-Wert Ihrer Daten.

Methode 3 von 3: SSE mit anderen statistischen Daten in Beziehung setzen

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 14

1. Berechnen Sie die Abweichung der SSE. Das Ermitteln der SSE für einen Datensatz ist im Allgemeinen ein Baustein, um andere, nützlichere Werte zu finden. Die erste davon ist die Varianz. Die Varianz ist ein Maß, das angibt, wie stark die gemessenen Daten vom Mittelwert abweichen. Es ist eigentlich der Mittelwert der quadrierten Differenzen vom Mittelwert.

Da die SSE die Summe der quadrierten Fehler ist, können Sie den Mittelwert (das ist die Varianz) einfach durch Division durch die Anzahl der Werte ermitteln. Wenn Sie jedoch die Varianz eines Stichprobensatzes und nicht einer gesamten Grundgesamtheit berechnen, teilen Sie die Varianz durch (n-1) statt durch n. So:

Varianz = SSE/n, wenn Sie die Varianz einer ganzen Grundgesamtheit berechnen.
Varianz = SSE/(n-1), wenn Sie die Varianz einer Datenstichprobe berechnen.

Für das Stichprobenproblem der Patiententemperatur können wir davon ausgehen, dass 10 Patienten nur eine Stichprobe bilden. Daher berechnet sich die Varianz dann wie folgt:

Abweichung = SSE (n - 1)

${displaystyle {text{Variation}}={frac {text{SSE}}{(n-1)}}}$

Abweichung = 6, 921 9

${displaystyle {text{Variation}}={frac {6.921}{9}}}$

Abweichung = 0, 769

${displaystyle {text{Variation}}=0,769}$

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 15

2. Berechnen Sie die Standardabweichung der SSE. Die Standardabweichung ist ein häufig verwendeter Wert, der angibt, wie stark die Werte eines Datensatzes vom Mittelwert abweichen. Die Standardabweichung ist die Quadratwurzel der Varianz. Beachten Sie, dass die Varianz der Mittelwert der quadrierten Fehlermaße ist.

Daher können Sie nach der Berechnung der SSE die Standardabweichung wie folgt ermitteln:

Standardabweichung = \sqrt{SSE} n - 1

${displaystyle {text{Standardabweichung}}={sqrt {frac {text{SSE}}{n-1}}}}$

Für die Stichprobe der Temperaturmessungen können Sie die Standardabweichung wie folgt ermitteln:

Standardabweichung = \sqrt{SSE} n - 1

${displaystyle {text{Standardabweichung}}={sqrt {frac {text{SSE}}{n-1}}}}$

Standardabweichung = \sqrt{\frac{6.921}{9}}

${displaystyle {text{Standardabweichung}}={sqrt {frac {text{6,921}}{9}}}}$

Standardabweichung = \sqrt{0, 769}

${displaystyle {text{Standardabweichung}}={sqrt {0.769}}}$

Standardabweichung = 0, 877

${displaystyle {text{Standardabweichung}}=0,877}$

Bild mit dem Titel Berechnen Sie die Summe der Fehlerquadrate (SSE) Schritt 16

3. Verwenden Sie SSE, um die Kovarianz zu bestimmen. Dieser Artikel konzentrierte sich auf Datensätze, die jeweils nur einen einzelnen Wert messen. In vielen Studien vergleichen Sie jedoch möglicherweise zwei separate Werte. Sie möchten beispielsweise wissen, wie sich diese beiden Werte zueinander verhalten, nicht nur zum Durchschnitt des Datensatzes. Dieser Wert ist die Kovarianz.

Die Berechnungen für die Kovarianz sind zu detailliert, um hier beschrieben zu werden, außer dass Sie die SSE für jeden Datentyp verwenden und dann vergleichen. Eine detailliertere Beschreibung der Kovarianz und der damit verbundenen Berechnungen finden Sie unter finde Artikel zu diesem Thema auf wikiHow.

Als Beispiel für die Verwendung der Kovarianz könnten Sie das Alter der Patienten in einer medizinischen Studie mit der Wirksamkeit eines Medikaments bei der Senkung der Fiebertemperatur vergleichen. Dann haben Sie einen Datensatz für das Alter und einen zweiten Datensatz für die Temperaturen. Sie finden dann die SSE für jeden Datensatz und daraus die Varianz, Standardabweichungen und Kovarianz.