Berechnung des standardfehlers

1. Die Standardabweichung. Die Standardabweichung einer Stichprobe gibt den Streuungsgrad der Zahlen an. Die Standardabweichung einer Stichprobe wird normalerweise mit einem s . bezeichnet. Die mathematische Formel für die Standardabweichung ist oben gezeigt.

2. Die Bevölkerung meint. Der Populationsmittelwert ist der Mittelwert eines Satzes numerischer Daten, der alle Werte der gesamten Gruppe enthält – mit anderen Worten, der Mittelwert eines vollständigen Zahlensatzes und nicht einer Stichprobe.

3. Das arithmetische Mittel. Dies ist nur ein Durchschnitt: die Summe einer Anzahl von Werten, geteilt durch dieselbe Anzahl von Werten.

4. Mustermittel erkennen. Wenn ein arithmetisches Mittel auf einer Reihe von Beobachtungen basiert, die durch Ziehen einer Stichprobe einer statistischen Grundgesamtheit gewonnen wurden, wird es als „Stichprobenmittel“ bezeichnet.” Dies ist der Durchschnitt eines numerischen Datensatzes, in dem einige der Werte innerhalb einer Gruppe enthalten sind. Es wird bezeichnet als:

5. Die Normalverteilung. Die Normalverteilung, die am häufigsten verwendete aller Verteilungen, ist symmetrisch, mit einem Ausreißer im Mittelwert der Daten. Die Form des Graphen ist die einer Uhr, wobei die Steigung auf beiden Seiten der Spitze gleich ist. Fünfzig Prozent der Verteilung sind links und fünfzig Prozent rechts. Die Verteilung einer Normalverteilung wird durch die Standardabweichung bestimmt.

6. Die Standardformel. Die Formel für den Standardfehler eines Stichprobenmittelwerts ist oben angegeben.

1. Berechnen Sie den Stichprobenmittelwert. Um den Standardfehler zu bestimmen, müssen Sie zuerst die Standardabweichung berechnen (da die Standardabweichung s Teil der Formel für den Standardfehler ist). Beginnen Sie mit der Berechnung des Mittelwerts der Beispielwerte. Der Stichprobenmittelwert wird als arithmetischer Mittelwert der Messungen x1, x2 . ausgedrückt, . . . xn. Dies wird mit der obigen Formel berechnet.

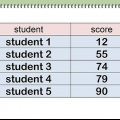
• Angenommen, Sie müssen den Standardfehler eines Stichprobenmittelwerts für die Messungen des Gewichts von fünf Münzen berechnen, wie in der folgenden Tabelle aufgeführt:
  Sie würden dann den Stichprobenmittelwert berechnen, indem Sie die Gewichtswerte wie folgt in die Formel eingeben:

2. Ziehen Sie den Stichprobenmittelwert von jeder Messung ab und quadrieren Sie diesen Wert. Sobald Sie den Stichprobenmittelwert haben, können Sie die Tabelle erweitern, indem Sie ihn von jeder einzelnen Messung subtrahieren und dann das Ergebnis quadrieren.

3. Bestimmen Sie die Gesamtabweichung Ihrer Messwerte vom Probenmittelwert. Die Gesamtabweichung ist der Mittelwert der quadrierten Differenz vom Stichprobenmittelwert. Addiere alle Werte zusammen um dies zu bestimmen.

4. Berechnen Sie die mittlere quadratische Abweichung der Messwerte vom Stichprobenmittelwert. Sobald Sie die Gesamtabweichung kennen, können Sie die mittlere Abweichung mit n -1 . ermitteln. Beachten Sie, dass n der Anzahl der Messungen entspricht.

5. Bestimmen Sie die Standardabweichung. Sie haben jetzt alle notwendigen Werte, um die Formel für die Standardabweichung(en) zu verwenden.

1. Verwenden Sie die Standardabweichung, um den Standardfehler mit der Standardformel zu berechnen.

• Im obigen Beispiel berechnen Sie den Standardfehler wie folgt:
  Der Standardfehler (die Standardabweichung des Stichprobenmittelwerts) beträgt also 0,0032031 Gramm.

Tipps

• Standardfehler und Standardabweichung werden oft verwechselt. Beachten Sie, dass der Standardfehler eine Beschreibung der Standardabweichung der Stichprobenverteilung eines statistischen Werts ist, nicht die Verteilung der einzelnen Werte.
• In wissenschaftlichen Zeitschriften werden Standardfehler und Standardabweichung manchmal synonym verwendet. Ein ±-Zeichen wird verwendet, um die beiden Messwerte zu verbinden.