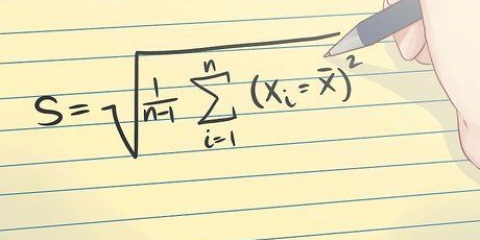Das Vertrauensintervall berechnen: 6 Schritte (mit Bildern)

Schritte
Tipps
Notwendigkeiten

Das Konfidenzintervall ist ein Indikator für die Genauigkeit Ihrer Messwerte. Es zeigt auch an, wie stabil Ihre Schätzung ist; der Grad, in dem Ihre Messwerte mit Ihrer Schätzung übereinstimmen, wenn Sie das Experiment wiederholen würden. Führen Sie die folgenden Schritte aus, um das Konfidenzintervall für Ihre Daten zu berechnen.

Schritte

Bildtitel Calculate Confidence Interval Step 1

1. Schreiben Sie das Phänomen auf, das Sie testen möchten. Angenommen, Sie arbeiten mit der folgenden Situation: Das Durchschnittsgewicht eines männlichen Universitätsstudenten A beträgt 180 Pfund. Sie testen nun, wie genau Sie das Gewicht der männlichen Studenten der Universität A mit einem vorgegebenen Konfidenzintervall vorhersagen können.

Bildtitel Calculate Confidence Interval Step 2

2. Nehmen Sie eine Probe aus Ihrer gewählten Population. Dies ist, was Sie verwenden werden, um die Daten zu sammeln, um Ihre Hypothese zu testen. Angenommen, Sie haben 1000 zufällige Schüler ausgewählt.

Bildtitel Calculate Confidence Interval Step 3

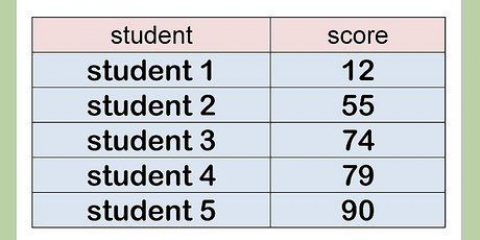
3. Berechnen Sie den Stichprobenmittelwert und die Standardabweichung. Wählen Sie eine Stichprobe (d. h. den Stichprobenmittelwert und die Standardabweichung), die Sie für die Schätzung des ausgewählten Populationsparameters verwenden möchten. Ein Populationsparameter ist ein bestimmtes Merkmal der Population. Hier sind der Stichprobenmittelwert und die Standardabweichung:

Um den Stichprobenmittelwert der Daten zu berechnen, addieren Sie alle Gewichte der von Ihnen ausgewählten 1000 Männer und dividieren Sie das Ergebnis durch 1000, die Anzahl der Männer. Der Durchschnitt in diesem Beispiel beträgt 180 Pfund.

Um die Standardabweichung zu berechnen, müssen Sie den Mittelwert der Daten berechnen. Jetzt ist es notwendig, die Varianz der Daten zu berechnen, auch bekannt als Mittelwert des Quadrats der Differenzen vom Mittelwert. Wenn Sie diese Zahl gefunden haben, ziehen Sie ihre Quadratwurzel ab. Angenommen, die Standardabweichung beträgt 30 Pfund. (Manchmal ist dies mit einer Aufgabe gegeben.)

Bildtitel Calculate Confidence Interval Step 4

4. Wählen Sie das gewünschte Konfidenzniveau. Die am häufigsten verwendeten Konfidenzniveaus sind 90 Prozent, 95 Prozent und 99 Prozent. Es ist auch möglich, dass dies mit einer Aufgabe gegeben ist. Angenommen, Sie haben 95 % gewählt.

Bildtitel Calculate Confidence Interval Step 5

5. Berechnen Sie die Fehlerspanne. Sie können die Fehlerquote mit der folgenden Formel ermitteln: z_a/2 * /√(n).z_a/2 = Konfidenzkoeffizient, wobei a = Konfidenzniveau, σ = Standardabweichung und n = Stichprobenumfang. Dies ist eine weitere Möglichkeit, anzuzeigen, dass Sie den kritischen Wert mit dem Standardfehler multiplizieren müssen.Sie lösen die Formel wie folgt, indem Sie sie teilen:

Bestimmen Sie den kritischen Wert, Z_a/2: Das Konfidenzniveau beträgt 95 %. Wandeln Sie diesen Prozentsatz in eine Dezimalzahl von 0,95 um und teilen Sie ihn durch 2, um 0,475 . zu erhalten. Dann schau im nächsten z-Tabelle um den Wert zu finden, der 0,475 . entspricht. Der nächste Wert ist 1,96, am Schnittpunkt von Zeile 1,9 und Spalte 0,06.

Um den Standardfehler zu ermitteln, nimm die Standardabweichung 30 und dividiere sie durch die Quadratwurzel des Stichprobenumfangs (1000). Sie erhalten jetzt 30/31,6 = 0,95 Pfund.

Multiplizieren Sie 1,96 mit 0,95 (der kritische Wert mal den Standardfehler) und Sie erhalten 1,86 oder die Fehlerspanne.

Bildtitel Calculate Confidence Interval Step 6

6. Geben Sie nun das Konfidenzintervall an. Nehmen Sie dazu den Mittelwert (180) und notieren Sie ihn neben dem ± und der Fehlerspanne. Die Antwort lautet: 180 ± 1,86. Sie können die obere und untere Grenze des Konfidenzintervalls finden, indem Sie die Fehlerspanne vom Mittelwert addieren und subtrahieren. Die Untergrenze beträgt also 180 – 1,86 oder 178,14 und die Obergrenze 180 + 1,86 oder 181,86.

Sie können auch die folgende praktische Formel verwenden, um das Konfidenzintervall zu ermitteln: x̅ ± Z_a/2 * /√(n). Hier steht x̅ für den Mittelwert.

Tipps

Sowohl t-Scores als auch Z-Scores können manuell, mit einem Taschenrechner oder mit statistischen Tabellen berechnet werden. Z-Scores können auch mit dem Normalverteilungsrechner bestimmt werden und t-Scores mit dem t-Verteilungsrechner. Online-Tools sind ebenfalls verfügbar.
Die Stichprobenpopulation muss für ein korrektes Konfidenzintervall normal sein.
Der kritische Wert, der zur Berechnung der Fehlerspanne verwendet wird, ist eine Konstante, ausgedrückt als t-Wert oder als z-Wert. T-Scores werden normalerweise gegenüber der Populationsstandardabweichung bevorzugt, ist unbekannt oder wenn eine kleine Stichprobe verwendet wird.
Es gibt viele Methoden, z. B. Zufallsstichproben, systematische Stichproben und geschichtete Stichproben, mit denen Sie eine repräsentative Stichprobe für die Hypothesenprüfung ziehen können.
Ein Konfidenzintervall sagt nichts über die Wahrscheinlichkeit eines bestimmten Ergebnisses aus. Wenn Sie beispielsweise zu 95 % sicher sind, dass der Mittelwert der Grundgesamtheit zwischen 75 und 100 liegt, bedeutet das 95 %-Konfidenzintervall nicht, dass der Mittelwert mit einer Wahrscheinlichkeit von 95 % in den berechneten Bereich fällt.