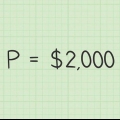Zinseszins berechnen: 15 Schritte (mit Bildern)

Schritte
Tipps

Der Zinseszins unterscheidet sich vom einfachen Zins darin, dass die Zinsrendite sowohl auf die ursprüngliche Investition (Kapital) als auch auf die bisher aufgelaufenen Zinsen und nicht nur auf den Kapitalbetrag berechnet wird. Deshalb wachsen Zinseszinskonten schneller als einfache Zinskonten. Außerdem wächst der Wert noch schneller, wenn die Zinsen mehrmals im Jahr aufgezinst werden. Zinseszinsen (auch Zinsen genannt) findet man bei verschiedenen Anlageprodukten und auch als Zinsen bei bestimmten Kreditarten, wie beispielsweise Kreditkartenschulden. Mit den richtigen Gleichungen ist es sehr einfach zu berechnen, wie viel ein Betrag durch Zinseszinsen wachsen wird.

Schritte

Teil 1 von 3: Berechnung des jährlichen Zinseszinses

Bildtitel Zinseszins berechnen Schritt 1

1. Definieren Sie den jährlichen Zinseszins. Der in Ihrem Anlageprospekt oder Kreditvertrag angegebene Zinssatz ist auf Jahresbasis. Wenn Sie beispielsweise einen Autokredit mit 6 % Zinsen aufnehmen, zahlen Sie 6 % Zinsen pro Jahr. Der Zinseszins zum Jahresende ist die einfachste Zinseszinsberechnung.

Der Zinseszins einer Schuld kann jährlich, monatlich oder sogar täglich berechnet werden.
Je öfter Ihre Schulden aufgezinst werden, desto schneller fallen Ihre Zinsen an.
Sie können den Zinseszins aus Anleger- oder Schuldnersicht betrachten. Häufig berechnete Zinseszinsen bedeuten, dass die Zinserträge der Anleger schneller wachsen. Es bedeutet auch, dass der Schuldner mehr Zinsen auf eine ausstehende Schuld schuldet.
Bei einem Sparkonto können beispielsweise die Zinsen jährlich berechnet werden, während die Zinsen bei einem Blitzkredit monatlich oder sogar wöchentlich berechnet werden können.

Bildtitel Zinseszins berechnen Schritt 2

2. Berechnen Sie den jährlichen Zinseszins für das Jahr 1. Angenommen, Sie besitzen eine Staatsanleihe im Wert von 1 €.000, zu einem Zinssatz von 6%. Staatsanleihen zahlen jedes Jahr Dividenden basierend auf Zinsen und Barwert.

Die Zinsen für Jahr 1 betragen dann 60 € (1 €.000 x 6%).

Um die Zinsen für Jahr 2 zu berechnen, müssen Sie den ursprünglichen Kapitalbetrag zu den bisherigen Gesamtzinsen addieren. In diesem Fall beträgt das Kapital des zweiten Jahres 1 €.060 (1€.000 + 60 €). Der Wert der Anleihe beträgt somit 1 €.060 und die zu zahlenden Zinsen werden anhand dieses Wertes berechnet.

Bildtitel Zinseszins berechnen Schritt 3

3. Berechnen Sie den Zinseszins für spätere Jahre. Um die größeren Auswirkungen des Zinseszinses zu sehen, berechnen Sie die Zinsen für spätere Jahre. Der Auftraggeber wächst von Jahr zu Jahr.

Multiplizieren Sie den Kapitalbetrag von Jahr 2 mit dem Zinssatz der Anleihe ($1.060 x 6% = 63,60 €). Die erhaltenen Zinsen sind 3,60 € höher (63,60 € - 60,00 €). Das liegt daran, dass das Kapital von 1 gestiegen ist.000 bis 1 €.060.

Für Jahr 3 beträgt das Kapital 1 €.123,60 (1 € .).060 + 63,60 €). Die Zinsen für Jahr 3 betragen 67,42 €. Dieser Betrag wird dem Kapital für die Berechnung von Jahr 4 hinzugefügt.

Je länger eine Schuld aussteht, desto größer ist die Auswirkung des Zinseszinses. Ausstehend bedeutet, dass die Schuld noch vom Schuldner beglichen werden muss.

Ohne Zinseszinsen würden die im Jahr 2 verdienten Zinsen 60 USD (1 € .) betragen.000 x 6%). Tatsächlich würden die Zinsen jedes Jahr 60 USD betragen, wenn Sie Zinseszinsen erhalten würden. Dies wird als einfaches Interesse bezeichnet.

Bildtitel Zinseszins berechnen Schritt 4

4. Erstellen Sie ein Excel-Dokument zur Berechnung des Zinseszinses. Es kann nützlich sein, den Zinseszins zu visualisieren, indem Sie ein einfaches Excel-Modell des Wachstums Ihrer Investition erstellen. Beginnen Sie mit dem Öffnen eines Dokuments und beschriften Sie die oberste Zelle in den Spalten A, B und C als "Jahr", "Wert" bzw. "Erworbene Zinsen".

Geben Sie die Jahre (0-5) in die Zellen A2 bis A7 ein.

Geben Sie den Prinzipal in Zelle B2 ein. Angenommen, Sie haben mit 1 € angefangen.000. Typ 1000.

Geben Sie in Zelle B3 `= B2 *1,06` ein und drücken Sie die Eingabetaste. Das bedeutet, dass Ihre Zinsen jährlich mit 6% (0,06) verzinst werden. Klicken Sie auf die untere rechte Ecke von Zelle B3 und ziehen Sie die Formel in Zelle B7. Die Zahlen sind jetzt richtig ausgefüllt.

Platziere eine 0 in Zelle C2. Geben Sie in Zelle C3 `=B3-B2` ein und drücken Sie die Eingabetaste. Dies ergibt die Differenz zwischen den Werten in den Zellen B3 und B2, die das Interesse darstellt. Klicken Sie auf die untere rechte Ecke von Zelle C3 und ziehen Sie die Formel in Zelle C7. Die Werte sollten automatisch ausgefüllt werden.

Wiederholen Sie diesen Vorgang so viele Jahre, wie Sie den Überblick behalten möchten. Sie können auch Kapital- und Zinssatzwerte einfach ändern, indem Sie die verwendeten Formeln und Zellinhalte ändern.

Teil 2 von 3: Berechnung des Zinseszinses bei Anlagen

Bildtitel Zinseszins berechnen Schritt 5

1. Lernen Sie die Zinseszinsformel. Die Zinseszinsformel berechnet den zukünftigen Wert der Anlage nach einer bestimmten Anzahl von Jahren. Die Formel selbst lautet wie folgt:

F V = P (1 + \frac{ich}{C})^{n * C}

$FV=P(1+{frac{i}{c}})^{{n*c}}$ Die Variablen innerhalb der Gleichung sind wie folgt definiert:

`FV` ist der zukünftige Wert. Das ist das Ergebnis der Rechnung.
`P` ist dein Prinzipal.
`i` ist der jährliche Zinssatz.
`c` ist der Zinseszinssatz (wie oft der Zinseszins jährlich berechnet wird).
`n` ist die zu berechnende Anzahl von Jahren.

Bildtitel Zinseszins berechnen Schritt 6

2. Sammle die Variablen für die Zinseszinsformel. Wenn Zinsen häufiger als jährlich berechnet werden, ist es schwierig, die Formel manuell zu berechnen. Sie können eine Zinseszinsformel für jede Berechnung verwenden. Um die Formel zu verwenden, benötigen Sie die folgenden Informationen:

Bestimmen Sie den Kapitalbetrag der Investition. Dies ist der ursprüngliche Betrag Ihrer Investition. Dies kann der Betrag sein, den Sie auf Ihr Konto eingezahlt haben, oder der ursprüngliche Kurs der Anleihe. Angenommen, Ihr Kapital auf einem Anlagekonto beträgt 5 €.000 ist.

Finden Sie den Zinssatz der Investition. Der Zinssatz muss ein Jahresbetrag sein, angegeben als Prozentsatz des Kapitalbetrags. Zum Beispiel ein Zinssatz von 3,45 % auf den Kapitalbetrag von 5 €.000.

Bei der Berechnung muss der Zinssatz als Dezimalzahl eingegeben werden. Wandeln Sie es um, indem Sie den Zinssatz durch 100 . dividieren. In diesem Beispiel wird es 3,45/100 = 0,0345.

Sie müssen auch wissen, wie oft die Zinsen aufgezinst werden. Die Zinsen werden normalerweise jährlich, monatlich oder täglich aufgezinst. Nehmen wir zum Beispiel an, es handelt sich um monatliche Zinsen. Das bedeutet, dass Ihr Zinssatz (`c`) als 12 . eingegeben werden muss.

Bestimmen Sie, über welchen Zeitraum Sie rechnen möchten. Dies könnte ein jährliches Wachstumsziel sein, beispielsweise 5 oder 10 Jahre, oder die Laufzeit der Anleihe. Das Fälligkeitsdatum einer Anleihe ist der Tag, an dem der Kapitalbetrag der Anlage zurückgezahlt werden muss. Als Beispiel verwenden wir hier zwei Jahre, also geben Sie eine 2 . ein.

Bildtitel Calculate Zinseszins Schritt 7

3. Verwenden Sie die Formel. Ersetzen Sie Ihre Variablen an den richtigen Stellen. Bitte überprüfen Sie, ob Sie sie richtig eingegeben haben. Achten Sie insbesondere darauf, dass die Zinsen dezimal eingegeben werden und Sie den richtigen Wert für `c` (Zinssatz) verwendet haben.

Das Anlagebeispiel wird dann wie folgt eingetragen:

F V = 5000 (1 + 0, 0345 12)^{2 * 12}

$FV=5000(1+{frac{0.0345}{12}})^{{2*12}}$

Berechnen Sie den Exponenten und den Teil der Formel in Klammern getrennt. Dies ist ein Konzept aus der Mathematik, das als "Reihenfolge der Operationen" bezeichnet wird. Du kannst Artikel über die Reihenfolge der Operationen auf wikiHow lesen.

Bildtitel Zinseszins berechnen Schritt 8

4. Vervollständige die mathematischen Berechnungen in der Formel. Vereinfachen Sie das Problem, indem Sie zuerst die Terme in Klammern lösen, beginnend mit dem Bruch.

Berechnen Sie zuerst den Bruch in Klammern. Das Ergebnis:

F V = 5000 (1 + 0, 00288) 2 * 12

$FV=5000(1+0,00288)^{{2*12}}$

Füge Zahlen in Klammern zusammen. Das Ergebnis:

F V = 5000 (1, 00288) 2 * 12

$FV=5000(1.00288)^{{2*12}}$

Lösen Sie die Multiplikation innerhalb des Exponenten (der letzte Teil über der schließenden Klammer). Das Ergebnis sollte so aussehen:

F V = 5000 (1, 00288) 24

$FV=5000(1.00288)^{{24}}$

Erhöhe die Zahl in Klammern mit dem Exponenten. Dies können Sie auf einem Taschenrechner tun, indem Sie zuerst den Wert in Klammern (1.00288 im Beispiel) eingeben und die Taste drücken

x ja

$x^{y}$ , und geben Sie dann den Exponenten ein (in diesem Fall 24), danach drücken Sie die Eingabetaste. Das Ergebnis dieses Beispiels ist

F V = 5000 (1, 0715)

$FV=5000(1,0715)$ .

Zum Schluss multiplizieren Sie das Prinzipal mit der Zahl in Klammern. Das Ergebnis im Beispiel beträgt 5 €.000 x 1,0715 = 5 €.357.50. Dies ist der Kontostand am Ende des zweiten Jahres.

Bildtitel Zinseszins berechnen Schritt 9

5. Subtrahiere den Hauptbetrag von deiner Antwort. Dies gibt den Zinsbetrag zurück.

Subtrahieren Sie das Kapital von 5 €.000 vom zukünftigen Wert von 5 €.357,50 und Sie erhalten 5 €.375,50 - 5 €.000 = 357,50 €

Sie haben nach zwei Jahren 357,50 € Zinsen verdient.

Teil 3 von 3: Berechnung des Zinseszinses bei regelmäßigen Zahlungen

Bildtitel Calculate Zinseszins Schritt 10

1. Lerne die Formel. Zinseszinsberechnungen können noch schneller wachsen, wenn Sie regelmäßige Einzahlungen tätigen, z. B. einen monatlichen Betrag auf ein Sparkonto überweisen. Die Formel ist länger als zur Berechnung des Zinseszinses ohne regelmäßige Zahlungen, folgt aber den gleichen Prinzipien. Die Formel lautet wie folgt:

F V = P (1 + \frac{ich}{C})^{n * C} + R ((1 + \frac{ich}{C})^{n * C} - 1) \frac{ich}{C}

$FV=P(1+{frac{i}{c}})^{{n*c}}+{frac{R((1+{frac{i}{c}})^{{n *c}}-1)}{{frac{i}{c}}}}$ Die Variablen in der Gleichung sind auch die gleichen wie in der vorherigen Gleichung, mit einer Ergänzung:

`P` ist das Prinzipal.
`i` ist der jährliche Zinssatz.
`c` ist die Zinsfrequenz und gibt an, wie oft die Zinsen jährlich aufgezinst werden.
`n` ist die Anzahl der Jahre.
`R` ist die Höhe des monatlichen Beitrags.

Bildtitel Zinseszins berechnen Schritt 11

2. Füllen Sie die Variablen aus. Um den zukünftigen Wert dieses Kontotyps zu berechnen, benötigen Sie den Kapitalbetrag (oder Barwert) des Kontos, den jährlichen Zinssatz, die Zinsfrequenz, die Anzahl der zu berechnenden Jahre und die Höhe Ihres monatlichen Beitrags. Diese Informationen sollten in Ihrem Investitionsvertrag enthalten sein.

Stellen Sie sicher, dass Sie den Jahreszins in eine Dezimalzahl umrechnen. Sie tun dies, indem Sie den Prozentsatz durch 100 . teilen. Nehmen wir zum Beispiel den obigen Zinssatz von 3,45% an, teilen wir 3,45 durch 100 und Sie erhalten 0,0345.

Für die Zinsfrequenz verwenden Sie die Anzahl der Berechnungen pro Jahr. Das bedeutet jährlich Nummer 1, monatlich 12 und täglich 365 (keine Sorge wegen Schaltjahren).

Bildtitel Calculate Zinseszins Schritt 12

3. Füllen Sie die Variablen aus. Wir fahren mit dem obigen Beispiel fort: Angenommen, Sie möchten 100 € pro Monat auf Ihr Konto überweisen. Über dieses Konto mit einem Kapital von 5 €.000, Zinseszins wird monatlich mit einem Jahreszins von 3,45% berechnet. Wir berechnen das Wachstum des Kontos über zwei Jahre.

Die endgültige Formel, die diese Informationen verwendet, lautet wie folgt:

F V = 5000 (1 + 0, 0345 12)^{2 * 12} + 100 ((1 + 0, 0345 12)^{2 * 12} - 1) \frac{0, 0345}{12}

$FV=5000(1+{frac{0,0345}{12}})^{{2*12}}+{frac{100((1+{frac{0,0345}{12}}) ^{{2 *12}}-1)}{{frac{0.0345}{12}}}}$

Bildtitel Zinseszins berechnen Schritt 13

4. Löse die Gleichung. Vergessen Sie auch hier nicht die richtige Reihenfolge der Operationen. Das bedeutet, Sie beginnen mit der Berechnung der Werte in den Klammern.

Lösen Sie zuerst die Brüche in den Klammern. Dies bedeutet, dass `i` durch `c` an drei Stellen geteilt wird, alle für das gleiche Ergebnis von 0,00288. Nun sieht die Gleichung so aus:

F V = 5000 (1 + 0, 00288) 2 * 12 + 100 ((1 + 0, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1+0,00288)^{{2*12}}+{frac{100((1+0,00288)^{{2*12}}-1)}{0,00288}}$

Löse die Addition in Klammern. Dies bedeutet, dass Sie die 1 zum Ergebnis des vorherigen Teils hinzufügen. Daher:

F V = 5000 (1, 00288) 2 * 12 + 100 ((1, 00288) 2 * 12 - 1) 0, 00288

$FV=5000(1.00288)^{{2*12}}+{frac{100((1.00288)^{{2*12}}-1)}{0.00288}}$

Lösen Sie die Multiplikation innerhalb der Exponenten. Dies bedeutet, dass die beiden Zahlen, die kleiner sind und über den schließenden Klammern liegen, multipliziert werden. Im Beispiel: 2 x 12 = 24. Daher:

F V = 5000 (1, 00288) 24 + 100 ((1, 00288) 24 - 1) 0, 00288

$FV=5000(1.00288)^{{24}}+{frac{100((1.00288)^{{24}}-1)}{0.00288}}$

Löse die Exponenten. Das bedeutet, den Betrag in Klammern mit dem Ergebnis des letzten Schrittes zu erhöhen. Auf einem Taschenrechner geschieht dies durch Eingabe des Wertes in Klammern (1.00288 im Beispiel), drücken Sie

x ja

$x^{y}$ und geben Sie den Wert des Exponenten ein (24). Daher:

F V = 5000 (1, 0715) + 100 (1, 0715 - 1) 0, 00288

$FV=5000(1,0715)+{frac{100(1,0715-1)}{0,00288}}$

subtrahieren. Subtrahiere 1 vom Ergebnis des letzten Schrittes im rechten Teil der Gleichung (1.0715 - 1). Daher:

F V = 5000 (1, 0715) + 100 (0, 0715) 0, 00288

$FV=5000(1.0715)+{frac{100(0.0715)}{0.00288}}$

Multiplizieren. Dies bedeutet, dass der Kapitalbetrag mit dem Wert in der ersten Klammer und der monatliche Beitrag mit dem gleichen Wert in Klammern multipliziert werden. Daher:

F V = 5357, 50 + 7, fünfzehn 0, 00288

$FV=5357.50+{frac{7.15}{0.00288}}$

Teilen Sie den Bruch. Daher:

F V = 5357, 50 + 2482, 64

$FV=5357,50+2482,64$

Addieren. Zum Schluss addieren Sie die beiden Zahlen zusammen, um den zukünftigen Wert des Kontos zu erhalten. Also: 5€.357,50 + 2 €.482,64 = 7 €.840.14. Dies ist der Wert des Kontos nach den zwei Jahren.

Bildtitel Zinseszins berechnen Schritt 14

5. Subtrahieren Sie den Kapitalbetrag und die Zahlungen. Um die erhaltenen Zinsen zu berechnen, müssen Sie den eingezahlten Betrag abziehen. Dies bedeutet, dass das Kapital 5 € . addiert wird.000, zum Gesamtwert der eingezahlten Beträge, also: 24 Beiträge (2 Jahre x 12 Monate/Jahr) mal die 100 €, die Sie jeden Monat eingezahlt haben, also insgesamt 2400 €. Die Summe beträgt 5 €.000 + 2 €.400 = 7400 €. Ziehe 7 €.400 € Rabatt auf den zukünftigen Wert von 7 €.840,14, und Sie haben den Zinsbetrag, 440,14 €.

Bildtitel Zinseszins berechnen Schritt 15

6. Erweitern Sie Ihre Berechnung. Um die Vorteile des Zinseszinses wirklich zu sehen, stellen Sie sich vor, dass Sie 20 Jahre lang (statt zwei) jeden Monat Geld auf dasselbe Konto einzahlen. In diesem Fall beträgt der zukünftige Wert etwa 45.000 Dollar, obwohl Sie nur 29 € ausgeben.000, was bedeutet, dass Ihre aufgelaufenen Zinsen 16 € betragen.000 beträgt.

Tipps

Sie können den Zinseszins auch ganz einfach mit einem Online-Zinsrechner berechnen. Ein Beispiel findet sich auf der Website der US-Regierung: https://www.Investor.gov/tools/calculators/compound-interest-calculator.
Eine schnelle Methode zur Bestimmung des Zinseszinses ist die 72-Regel. Beginnen Sie, indem Sie 72 durch den Zinsbetrag teilen, den Sie erhalten, sagen wir 4%. Also in diesem Fall 72/4 = 18. Dieses Ergebnis, 18, entspricht ungefähr der Anzahl von Jahren, die Sie benötigen, um Ihre Investition zum aktuellen Zinssatz zu verdoppeln. Denken Sie daran, dass die 72-Regel nur eine schnelle Annäherung ist, kein genaues Ergebnis.
Sie können diese Berechnungen auch verwenden, um "Was wäre wenn"-Berechnungen durchzuführen, die Ihnen sagen können, wie viel Sie je nach Zinssatz, Kapital, Zinssatz oder Anzahl der Jahre verdienen werden.

"Zinseszins berechnen"

Zinsen berechnen

Inflation berechnen

Berechnen sie die gesamtzinsen für einen autokredit

Bruttoinlandsprodukt berechnen

Оцените, пожалуйста статью