Angenommen, Sie haben einem Freund Geld geliehen mit der Vereinbarung, dass er nach sechs Monaten die 2000 $ mit einem Zins von 1,5 % zurückzahlt. Der Einmalzins beträgt 1,5 %. Aber bevor Sie den Prozentsatz von 1,5% verwenden können, müssen Sie ihn in eine Dezimalzahl umwandeln. Um Prozent in Dezimalzahlen umzuwandeln, teilen Sie den Prozentsatz durch 100: 1,5% 100=0,015. 
Wichtig ist, dass die Laufzeit dem Zinssatz entspricht oder zumindest in den gleichen Einheiten gemessen wird. Beispiel: Handelt es sich um einen Jahreszins, dann muss Ihre Laufzeit auch in Jahren bemessen werden. Wenn der Zinssatz mit 3 % pro Jahr ausgeschrieben ist, das Darlehen jedoch nur für sechs Monate läuft, berechnen Sie einen jährlichen Zinssatz von 3 % über einen Zeitraum von 0,5 Jahren. Ein anderes Beispiel: Wenn der vereinbarte Zinssatz 1 % pro Monat beträgt und Sie sich das Geld für sechs Monate leihen, beträgt die Laufzeit für die Berechnung sechs Monate. 

Im obigen Beispiel des Darlehens an einen Freund hat der Auftraggeber ( ) gleich $2000 und der Prozentsatz (
) gleich $2000 und der Prozentsatz ( ) beträgt 0,015 über einen Zeitraum von sechs Monaten. Da der Vertrag in diesem Beispiel eine Laufzeit von sechs Monaten hatte, ist die Variable
) beträgt 0,015 über einen Zeitraum von sechs Monaten. Da der Vertrag in diesem Beispiel eine Laufzeit von sechs Monaten hatte, ist die Variable  in diesem Fall 1. Berechnen Sie dann die Zinsen wie folgt:
in diesem Fall 1. Berechnen Sie dann die Zinsen wie folgt:  . Die fälligen Zinsen betragen also 30 €.
. Die fälligen Zinsen betragen also 30 €.Wenn Sie den vollen geschuldeten Betrag (A) mit den Zinsen und dem Erlös des Kapitals berechnen möchten, verwenden Sie die Formel  . Diese Berechnung sieht so aus:
. Diese Berechnung sieht so aus: 








In drei Monaten würden Sie 37,50 € Zinsen verdienen. Beachten Sie, dass t=0,25 ist, da drei Monate ein Viertel (0,25) des ursprünglichen Zeitraums von einem Jahr sind. 


Zum Beispiel kann ein Kreditkartenunternehmen seine Zinsen mit 15 % pro Jahr ausweisen. Die Zinsen werden jedoch in der Regel monatlich berechnet, daher möchten Sie wahrscheinlich wissen, wie hoch der monatliche Zinssatz ist. In diesem Fall teilen Sie es durch 12 und Sie erhalten eine monatliche Verzinsung von 1,25%. Diese beiden Prozentsätze, 15% pro Jahr und 1,25% pro Monat, sind einander gleich. 
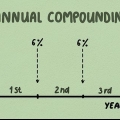
Wenn die Zinsen jährlich aufgezinst werden, dann ist n=1. Wenn Zinsen vierteljährlich aufgezinst werden, dann Geld n=4. 
Beispiel: bei einem Kredit für ein Jahr,  . Bei einer Laufzeit von 18 Monaten
. Bei einer Laufzeit von 18 Monaten  .
. 
Bestimmen Sie zuerst, welche Variablen Sie benötigen, um das Problem zu lösen. In diesem Fall: 




Bei obigem Problem sieht das so aus: 





Sie haben also nach drei Jahren Zinseszins einen Betrag von 808 € zusätzlich zu den ursprünglich eingezahlten 5000 €. 

 ist der zukünftige Wert (oder Betrag) des Geldes, den das Darlehen nach Aufzinsung der Zinsen wert sein wird.
ist der zukünftige Wert (oder Betrag) des Geldes, den das Darlehen nach Aufzinsung der Zinsen wert sein wird. ist der Schulleiter.
ist der Schulleiter.Die Konstante  . Obwohl es wie eine Variable aussieht, ist es tatsächlich eine Konstante. Der Buchstabe
. Obwohl es wie eine Variable aussieht, ist es tatsächlich eine Konstante. Der Buchstabe  ist eine spezielle Zahl, die "Eulersche Konstante" genannt wird, nach dem Mathematiker Leonard Euler, der ihre Eigenschaften entdeckt hat.
ist eine spezielle Zahl, die "Eulersche Konstante" genannt wird, nach dem Mathematiker Leonard Euler, der ihre Eigenschaften entdeckt hat. Die meisten fortgeschrittenen Grafikrechner haben eine Taste für  . Wenn Sie diese Taste mit der Nummer 1 drücken, also
. Wenn Sie diese Taste mit der Nummer 1 drücken, also  , dann sehen Sie, dass der Wert von
, dann sehen Sie, dass der Wert von  ist ungefähr 2.718.
ist ungefähr 2.718.  sind die Zinsen pro Jahr.
sind die Zinsen pro Jahr. ist die Laufzeit des Darlehens in Jahren.
ist die Laufzeit des Darlehens in Jahren.

 , wieder keine Variable, sondern die Konstante 2.718.
, wieder keine Variable, sondern die Konstante 2.718.







Beachten Sie den enormen Wert des revolvierenden Zinseszinses.
Zinsen berechnen
Die meisten Leute kennen den Begriff des Zinses, aber nicht jeder weiß, wie man ihn berechnet. Zinsen sind der Mehrwert eines Darlehens oder Vorschusses, um die Verwendung des Geldes anderer Personen über einen bestimmten Zeitraum zu bezahlen. Zinsen können auf drei Arten berechnet werden. Normalzins ist am einfachsten zu berechnen und gilt generell für kurzfristige Kredite. Der Zinseszins ist etwas komplizierter und mehr wert. Schließlich wächst die konstante Verzinsung am schnellsten und diese Formel verwenden die meisten Banken für Hypothekendarlehen. Die Informationen, die Sie für all diese Berechnungen benötigen, sind im Allgemeinen gleich, aber die Mathematik ist für jede ein wenig anders.
Schritte
Methode 1 von 3: Berechnung einfacher Zinsen

1. Bestimmen Sie den Kapitalbetrag. Der Kapitalbetrag ist der Geldbetrag, den Sie verwenden, um die Zinsen zu berechnen. Dies kann ein Betrag sein, den Sie auf ein Sparkonto einzahlen oder in eine Art Anlage investieren. In diesem Fall können Sie die Zinsen berechnen, die Sie verdienen. Die Alternative besteht darin, dass wenn Sie sich Geld leihen, beispielsweise für eine Hypothek, der Kapitalbetrag der Betrag ist, den Sie sich leihen, und Sie können die Zinsen berechnen, die Sie schulden.
- Unabhängig davon, ob Sie Zinsen einziehen oder zahlen, wird der Kapitalbetrag in jedem Fall durch die Variable P . symbolisiert.
- Wenn Sie sich beispielsweise 2.000 USD von einem Freund geliehen haben, sind diese 2.000 USD der Hauptbetrag.

2. Bestimmen Sie das Interesse. Bevor Sie berechnen können, wie stark der Kapitalwert steigen wird, müssen Sie den Zinssatz kennen, zu dem der Kapitalwert steigen wird. Das ist dein Interesse. Die Zinsen werden in der Regel vor der Kreditvergabe ausgeschrieben oder zwischen den Parteien vereinbart.

3. Prüfen Sie die Laufzeit des Darlehens. Die Laufzeit ist eine andere Bezeichnung für die Laufzeit des Darlehens. In einigen Fällen stimmen Sie der Laufzeit des Darlehens zu, indem Sie den Betrag leihen. Beispiel: Die meisten Hypotheken haben eine feste Laufzeit. In vielen Fällen vereinbaren Kreditnehmer und Kreditgeber bei einem Privatkredit eine vorab vereinbarte Laufzeit.

4. Berechnen Sie die Zinsen. Um die Zinsen zu berechnen, multiplizieren Sie den Kapitalbetrag mit dem Zinssatz und der Laufzeit des Darlehens. Diese Formel kann algebraisch ausgedrückt werden als:

 ) gleich $2000 und der Prozentsatz (
) gleich $2000 und der Prozentsatz ( ) beträgt 0,015 über einen Zeitraum von sechs Monaten. Da der Vertrag in diesem Beispiel eine Laufzeit von sechs Monaten hatte, ist die Variable
) beträgt 0,015 über einen Zeitraum von sechs Monaten. Da der Vertrag in diesem Beispiel eine Laufzeit von sechs Monaten hatte, ist die Variable  in diesem Fall 1. Berechnen Sie dann die Zinsen wie folgt:
in diesem Fall 1. Berechnen Sie dann die Zinsen wie folgt: . Die fälligen Zinsen betragen also 30 €.
. Die fälligen Zinsen betragen also 30 €. . Diese Berechnung sieht so aus:
. Diese Berechnung sieht so aus:




5. Versuchen Sie es mit einem anderen Beispiel. Angenommen, Sie legen 5.000 USD auf ein Sparkonto mit einer jährlichen Verzinsung von 3% ein. Nach nur drei Monaten heben Sie das Geld samt Zinsen ab.




Methode 2 von 3: Zinseszins berechnen

1. Verstehen Sie, was Zinseszinsen ist. Zinseszinsen bedeutet, dass, wenn Sie Zinsen verdienen, die Zinsen dem Betrag auf Ihrem Konto hinzugefügt werden und Sie beginnen, zusätzlich zu den Zinsen Zinsen zu verdienen (oder zu zahlen). Ein einfaches Beispiel: Wenn Sie 100 US-Dollar zu 5 % Zinsen pro Jahr einzahlen, haben Sie am Ende eines Jahres 5 US-Dollar Zinsen verdient. Wenn Sie dies Ihrem Konto wieder gutschreiben, haben Sie am Ende des zweiten Jahres 5 % von 105 US-Dollar verdient, nicht nur die ursprünglichen 100 US-Dollar. Im Laufe der Zeit kann dies sehr stark ansteigen.
- Die Formel zur Berechnung des Werts (A) des Zinseszinses lautet wie folgt:

2. Wissen, was der Prinzipal bedeutet. Wie bei einfachen Zinsen beginnt die Berechnung mit der Höhe des Kapitalbetrags. Die Berechnung ist gleich, egal ob Sie die Zinsen für geliehenes oder geliehenes Geld berechnen. Das Prinzipal wird im Allgemeinen durch die Variable  .
.
 .
.
3. Bestimmen Sie den Prozentsatz. Der Zinssatz muss vor der Kreditvergabe vereinbart und für die Berechnung als Dezimalzahl ausgewiesen werden. Wisse, dass der Prozentsatz in eine Dezimalzahl umgewandelt werden kann, indem du ihn durch 100 dividierst (oder schneller, indem du die Dezimalstelle um zwei Stellen nach links verschiebst). Stellen Sie sicher, dass Sie wissen, für welchen Zeitraum der Zinssatz gilt. Der Prozentsatz hat  als Symbol.
als Symbol.
 als Symbol.
als Symbol.
4. Wissen, wann die Zinsen aufgezinst werden. Zinseszinsen bedeutet, dass die Zinsen periodisch berechnet und dem Kapitalbetrag wieder hinzugerechnet werden. Bei manchen Krediten kann dies einmal im Jahr passieren. Bei anderen ist es jeden Monat oder jedes Quartal. Sie müssen wissen, wie oft die Zinsen pro Jahr aufgezinst werden.

5. Kennen Sie die Laufzeit des Darlehens. Die Laufzeit ist der Zeitraum, über den die Zinsen berechnet werden. Die Dauer wird in der Regel in Jahren angegeben. Wenn Sie die Zinsen über einen anderen Zeitraum berechnen müssen, müssen Sie diese in Jahre umrechnen.
 . Bei einer Laufzeit von 18 Monaten
. Bei einer Laufzeit von 18 Monaten  .
.
6. Bestimmen Sie die Variablen der Situation. Nehmen wir in diesem Beispiel an, Sie zahlen 5.000 $ auf ein Sparkonto mit einem monatlichen Zinseszins von 5 % ein. Wie hoch ist der Wert dieses Kontos nach drei Jahren??





7. Wenden Sie die Formel an und berechnen Sie den Zinseszins. Wenn Sie wissen, was zu tun ist und welche Variablen benötigt werden, wenden Sie diese auf die Formel zur Berechnung des Zinssatzes an.






Methode 3 von 3: Wiederkehrende Zinseszinsen berechnen

1. Verstehen Sie, was revolvierende Zinseszinsen sind. Wie Sie im vorherigen Beispiel gesehen haben, wächst der Zinseszins schneller als der einfache Zins, wodurch das Kapital zu bestimmten Zeiten verzinst wird. Vierteljährlich zu kompilieren ist wertvoller als jährlich. Die monatliche Zusammenstellung ist noch wertvoller als jährlich. Die profitabelste Situation wäre, wenn die Zinsen ständig aufgezinst werden, also jeden Moment. Sobald Zinsen berechnet werden können, werden diese dem Konto gutgeschrieben und dem Kapital gutgeschrieben. Dies ist natürlich nur ein theoretischer Fall.
- Mit ein wenig Mathematik haben Mathematiker eine Formel zur Simulation von Zinsen entwickelt, die kontinuierlich aufgezinst und dem Konto hinzugefügt werden. Diese Formel zur Berechnung des revolvierenden Zinseszinses lautet:

2. Kennen Sie die Variablen zur Zinsberechnung. Die Formel für revolvierende Zinseszinsen ist den vorherigen Situationen sehr ähnlich, jedoch mit einigen geringfügigen Anpassungen. Die Variablen für die Formel sind:
 ist der zukünftige Wert (oder Betrag) des Geldes, den das Darlehen nach Aufzinsung der Zinsen wert sein wird.
ist der zukünftige Wert (oder Betrag) des Geldes, den das Darlehen nach Aufzinsung der Zinsen wert sein wird. ist der Schulleiter.
ist der Schulleiter. . Obwohl es wie eine Variable aussieht, ist es tatsächlich eine Konstante. Der Buchstabe
. Obwohl es wie eine Variable aussieht, ist es tatsächlich eine Konstante. Der Buchstabe  ist eine spezielle Zahl, die "Eulersche Konstante" genannt wird, nach dem Mathematiker Leonard Euler, der ihre Eigenschaften entdeckt hat.
ist eine spezielle Zahl, die "Eulersche Konstante" genannt wird, nach dem Mathematiker Leonard Euler, der ihre Eigenschaften entdeckt hat. . Wenn Sie diese Taste mit der Nummer 1 drücken, also
. Wenn Sie diese Taste mit der Nummer 1 drücken, also  , dann sehen Sie, dass der Wert von
, dann sehen Sie, dass der Wert von  ist ungefähr 2.718.
ist ungefähr 2.718. sind die Zinsen pro Jahr.
sind die Zinsen pro Jahr. ist die Laufzeit des Darlehens in Jahren.
ist die Laufzeit des Darlehens in Jahren.
3. Kennen Sie die Details Ihres Darlehens. Banken verwenden normalerweise revolvierende Zinseszinsen für Hypotheken. Angenommen, Sie haben 200 €.000 wollen sich für eine Hypothek von 30 Jahren zu einem Zins von 4,2% leihen. Die Variablen, die Sie für diese Berechnung verwenden, sind also:

 , wieder keine Variable, sondern die Konstante 2.718.
, wieder keine Variable, sondern die Konstante 2.718.


4. Verwenden Sie die Formel zur Berechnung der Zinsen. Wenden Sie die Werte auf die Formel an, um den Zinsbetrag zu berechnen, den Sie für das 30-jährige Darlehen zahlen müssen.





Оцените, пожалуйста статью