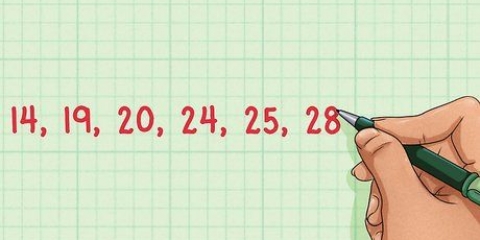Beispiel: `Anzahl Bücher` oben in der ersten Spalte. Schreiben Sie `Frequenz` oben in die zweite Spalte. Schreiben Sie in der zweiten Zeile den ersten Wert unter Anzahl Bücher: 3. Zählen Sie die Anzahl der Dreien in Ihrem Datensatz. Da es zwei Dreier gibt, geben Sie 2 unter Frequenz in derselben Zeile ein. Wiederholen Sie dies für jeden Wert, bis Sie die gesamte Tabelle ausgefüllt haben: 3 | F=2 5 | F=1 6 | F=3 8 | F=1 
Beispiel: Der niedrigste Wert ist drei. Die Zahl der Schüler, die drei Bücher gelesen haben, beträgt zwei. Niemand hat weniger Bücher gelesen, daher beträgt die kumulative Häufigkeit drei. Fügen Sie dies in die erste Zeile Ihrer Tabelle ein: 3 | F=2 | CF=2 
Beispiel: 3 | F=2 | CF=2 5 | F=1 | CF=2+1=3 
Beispiel: 3 | F=2 | CF=2 5 | F=1 | CF=2 + 1=3 6 | F=3 | CF=3 + 3=6 8 | F=1 | CF=6 + 1=7 
Einzelfrequenzen addieren: 2 + 1 + 3 + 1=7, unsere letzte kumulierte Frequenz. Zählen Sie die Anzahl der Datenpunkte. Unsere Liste war 3, 3, 5, 6, 6, 6, 8. Es gibt sieben Objekte, unsere ultimative kumulative Häufigkeit. 

Datensatz: 233, 259, 277, 278, 289, 301, 303 Tabelle (erste Spalte – Wert, zweite Spalte – Häufigkeit, dritte Spalte – kumulierte Häufigkeit): 200–250|1|1 251–300|4|1 + 4=5 301–350|2|5 + 2=7 
Beispiel: Wenn Ihr Datensatz von 1 bis 8 reicht, zeichnen Sie eine x-Achse mit acht markierten Einheiten. Zeichnen Sie auf jedem Wert der x-Achse einen Punkt auf dem y-Wert, der gleich der kumulativen Häufigkeit an diesem Punkt ist. Verbinden Sie jedes Paar benachbarter Punkte mit einer Linie. Wenn bei einem bestimmten Wert keine Datenpunkte vorhanden sind, ist die absolute Häufigkeit null. Das Hinzufügen von Null zur letzten kumulierten Häufigkeit ändert den Wert nicht, daher zeichnen wir einen Punkt am gleichen y-Wert wie der letzte Wert. Da die kumulierte Häufigkeit mit den Werten immer zunimmt, sollte Ihr Diagramm immer stabil bleiben oder nach rechts steigen. Wenn die Linie irgendwann untergeht, sehen Sie möglicherweise versehentlich eine absolute Frequenz. 
Betrachten Sie den letzten Punkt auf der rechten Seite des Diagramms. Der y-Wert ist die kumulative Gesamthäufigkeit, d. h. die Anzahl der Punkte im Datensatz. Angenommen, dieser Wert ist gleich 16. Multiplizieren Sie diesen Wert mit ½ und finden Sie ihn auf der y-Achse. In unserem Beispiel ist dies 8 (die Hälfte von 16). Finden Sie 8 auf der y-Achse. Finden Sie den Punkt im Diagramm bei diesem y-Wert. Bewegen Sie Ihren Finger von der 8 auf der y-Achse entlang des Diagramms. Stoppen Sie, wenn Ihr Finger die Linie des Diagramms berührt. Dies ist der Punkt, an dem genau die Hälfte Ihrer Datenpunkte gezählt wird. Bestimmen Sie den x-Wert an dieser Stelle. Bewegen Sie Ihren Finger gerade nach unten zur x-Achse. Dieser Wert ist der Median Ihres Datensatzes. Wenn dieser Wert beispielsweise 65 beträgt, liegt die Hälfte Ihres Datensatzes unter 65 und die andere Hälfte über 65 . 
Um den y-Wert des unteren Quartils zu ermitteln, nehmen Sie die maximale kumulative Häufigkeit und multiplizieren Sie sie mit ¼. Der entsprechende x-Wert ergibt den y-Wert, mit genau einem Viertel der Daten darunter. Um den y-Wert des oberen Quartils zu ermitteln, multiplizieren Sie die maximale kumulative Häufigkeit mit ¾. Der entsprechende x-Wert ergibt den y-Wert, mit genau drei Vierteln der Daten darunter und einem Viertel darüber.
Kumulative häufigkeit berechnen
In der Statistik bezieht sich die absolute Häufigkeit darauf, wie oft ein bestimmter Wert in einem Datensatz angezeigt wird. Die kumulative Häufigkeit ist anders: Sie ist die Summe (oder vorläufige Summe) aller Häufigkeiten bis zum aktuellen Punkt im Datensatz. Machen Sie sich keine Sorgen, wenn das wie Slang klingt; es ist ganz einfach, wenn du zu Stift und Papier greifst.
Schritte
Teil1 von 2: Bestimmung der kumulativen Grundfrequenz

1. Sortieren Sie den Datensatz. Ein „Datensatz“ ist nur die Gruppe von Zahlen, die Sie studieren. Sortieren Sie diese Werte vom kleinsten zum größten.
- Beispiel: Ihr Datensatz enthält die Anzahl der Bücher, die jeder Schüler im letzten Monat gelesen hat. Nach dem Sortieren ist dies der Datensatz: 3, 3, 5, 6, 6, 6, 8.

2. Zählen Sie die absolute Häufigkeit jedes Wertes. Die Häufigkeit eines Werts ist die Häufigkeit, mit der der Wert angezeigt wird (Sie können dies die `absolute Häufigkeit` nennen, wenn Sie eine Verwechslung mit der kumulativen Häufigkeit vermeiden möchten). Der einfachste Weg, den Überblick zu behalten, besteht darin, eine Tabelle zu erstellen. Geben Sie "Wert" (oder eine Beschreibung dessen, was der Wert misst) am Anfang der ersten Spalte ein. Schreiben Sie `Frequenz` oben in die zweite Spalte. Füllen Sie die Tabelle für jeden Wert aus.

3. Bestimmen Sie die kumulative Häufigkeit des ersten Wertes. Die kumulierte Häufigkeit beantwortet die Frage „Wie oft kommt dieser Wert? oder ein kleinerer Wert Pro?Beginnen Sie immer mit dem niedrigsten Wert in Ihrem Datensatz. Da es keine kleineren Werte gibt, entspricht die Antwort der absoluten Häufigkeit dieses Wertes.

4. Bestimmen Sie die kumulative Häufigkeit des folgenden Wertes. Weiter zum nächsten Wert in der Tabelle. Wir haben gerade herausgefunden, wie oft die niedrigeren Werte vorkommen. Um die kumulative Häufigkeit dieses Wertes zu bestimmen, müssen wir nur die absolute Häufigkeit zur laufenden Summe addieren. Mit anderen Worten, nehmen Sie die letzte gefundene kumulative Häufigkeit und addieren Sie die absolute Häufigkeit dieses Wertes dazu.

5. Wiederholen Sie dies für die anderen Werte. Mach weiter mit immer größeren Werten. Addiere jedes Mal die letzte kumulierte Häufigkeit zur absoluten Häufigkeit des nächsten Wertes.

6. Überprüfe deine Arbeit. Wenn Sie fertig sind, haben Sie die Anzahl der Instanzen jeder Variablen addiert. Die letzte kumulative Häufigkeit muss der Gesamtzahl der Datenpunkte in der Reihe entsprechen. Es gibt zwei Möglichkeiten, dies zu überprüfen:
Teil 2 von 2: Mehr aus den Daten machen

1. Diskrete und kontinuierliche Daten verstehen. Diskrete Daten werden in Einheiten geliefert, die Sie zählen können, wobei es unmöglich ist, einen Teil einer Einheit zu bestimmen. Kontinuierliche Daten beschreiben etwas, das nicht gezählt werden kann, mit Messungen, die irgendwo zwischen den von Ihnen gewählten Einheiten liegen können. Hier einige Beispiele:
- Anzahl der Hunde: diskret. Es gibt keinen halben Hund.
- Schneehöhe: kontinuierlich. Schnee baut sich nach und nach auf, nicht in einer Einheit nach der anderen. Wenn Sie versucht haben, es in Zentimetern zu messen, haben Sie möglicherweise eine 5,6 Zentimeter tiefe Schneeschicht gefunden.

2. Kontinuierliche Daten nach Bereich gruppieren. Kontinuierliche Datensätze haben oft eine große Anzahl eindeutiger Variablen. Der Versuch, die obige Methode zu verwenden, würde die Tabelle sehr lang und schwer verständlich machen. Machen Sie stattdessen jede Zeile Ihrer Tabelle zu einem Wertebereich. Es ist wichtig, dass jeder Bereich die gleiche Größe hat (z. B. 0-10, 11-20, 21-30 usw.).), egal wie viele Werte in jedem Bereich vorhanden sind. Hier ist ein Beispiel für einen kontinuierlichen Datensatz, der in eine Tabelle umgewandelt wurde:

3. Erstellen Sie ein Diagramm. Sobald Sie die kumulative Häufigkeit berechnet haben, greifen Sie zu Millimeterpapier. Zeichnen Sie ein Diagramm, bei dem die x-Achse den Werten Ihres Datensatzes entspricht und die y-Achse der kumulierten Häufigkeit entspricht. Dadurch werden die folgenden Berechnungen viel einfacher.

4. Finden Sie den Median des Graphen. Der Median ist der Wert, der genau in der Mitte des Datensatzes liegt. Die Hälfte der Werte liegt über dem Median, die andere Hälfte darunter. So finden Sie den Median in Ihrem Diagramm:

5. Bestimme die Quartile aus dem Graphen. Quartile unterteilen die Daten in vier Abschnitte. Dieser Vorgang ist der Bestimmung des Medians sehr ähnlich. Der einzige Unterschied besteht darin, wie Sie die y-Werte bestimmen:
Tipps
- Sie können jeden großen Datensatz in Bereichen anzeigen, auch wenn die Daten diskret sind.
Оцените, пожалуйста статью