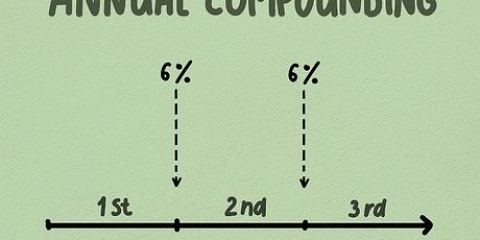
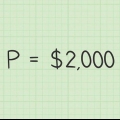Zinsen auf einem Sparkonto berechnen

Schritte
Tipps

Zwar lassen sich die Zinsen für Spareinlagen manchmal einfach berechnen, indem man den Zinssatz mit dem Eröffnungssaldo multipliziert, aber in den meisten Fällen ist es nicht so einfach. Beispiel: Viele Sparkonten weisen jährliche Zinsen aus, berechnen jedoch monatlich den Zinseszins. Jeden Monat wird ein Bruchteil der Jahreszinsen berechnet und Ihrem Guthaben gutgeschrieben, was sich wiederum auf die Berechnung der Folgemonate auswirkt. Dieser Zinszyklus, bei dem die Zinsen in Schritten berechnet und Ihrem Konto kontinuierlich hinzugefügt werden, wird Zinseszins genannt. Der einfachste Weg, den zukünftigen Saldo zu berechnen, ist die Verwendung einer Zinseszinsformel. Lesen Sie weiter, um die Besonderheiten dieser Arten von Zinsberechnungen zu erfahren.

Schritte

Methode 1 von 3: Zinseszins berechnen

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 1

1. Kennen Sie die Formel zur Berechnung des Zinseszinseffekts. Die Formel zur Berechnung der Zinseszinsakkumulation für einen bestimmten Saldo lautet:

ein = P (1 + (\frac{R}{n}))^{n * T}

$A=P(1+({frac{r}{n}}))^{{n*t}}$ .

(P) ist das Kapital, (r) ist der jährliche Zinssatz und (n) ist die Anzahl der Zinssätze pro Jahr. (A) ist der Saldo, auf dem Sie berechnen, einschließlich der Auswirkungen der Zinsen.
(t) stellt die Zeiträume dar, über die die Zinsen aufgelaufen sind. Er muss dem von Ihnen angenommenen Zinssatz entsprechen (wenn es sich beispielsweise um einen Jahreszins handelt, muss (t) eine Anzahl von Jahren als Bruch sein). Um die richtige Anzahl von Jahren als Bruch über einen bestimmten Zeitraum anzuzeigen, teilen Sie die Gesamtanzahl der Monate durch 12 oder dividieren Sie die Gesamtanzahl der Tage durch 365.

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 2

2. Bestimmen Sie die in der Formel verwendeten Variablen. Lesen Sie die AGB Ihres Privatkontos oder wenden Sie sich an einen Mitarbeiter Ihrer Bank, um den Vergleich abzuschließen.

Das Kapital (P) ist der erste auf das Konto eingezahlte Betrag oder der aktuelle Betrag, den Sie für die Zinsberechnung annehmen.

Der Zinssatz (r) muss in Dezimalform angegeben werden. Ein Zins von 3% muss als 0,03 . eingegeben werden. Teilen Sie dazu den angegebenen Zinssatz durch 100.

Der Wert von (n) gibt an, wie oft pro Jahr Zinsen berechnet und Ihrem Guthaben hinzugefügt werden (auch als Aufzinsung bekannt). Die Zinsen werden in der Regel monatlich (n=12), vierteljährlich (n=4) oder jährlich (n=1) aufgezinst, aber je nach Ihren spezifischen Kontobedingungen können andere Optionen verfügbar sein.

Bildtitel Calculate Bank Interest on Savings Step 3

3. Setze deine Werte in die Formel ein. Nachdem Sie die Werte für jede Variable ermittelt haben, können Sie diese in die Zinseszinsformel eingeben, um den Zinssatz über die vorgegebene Zeitskala zu bestimmen. Mit den Werten P=1000, r=0,05 (5%), n=4 (erstellt pro Quartal) und t=1 Jahr erhalten wir beispielsweise folgende Gleichung:

ein = 1000 (1 + (0, 05 4))^{4 * 1}

$A=1000(1+({frac{0,05}{4}}))^{{4*1}}$ .

Der tägliche Zinseszins wird auf ähnliche Weise bestimmt, außer dass Sie dann die 4, wie oben für Variable(n) verwendet, durch 365 . ersetzen würden.

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 4

4. Mach die Berechnung. Nachdem die Zahlen eingegeben wurden, ist es an der Zeit, die Formel zu lösen. Beginnen Sie mit der Vereinfachung der einfachen Teile der Gleichung. Teilen Sie den Jahreszinssatz durch die Anzahl der Raten, um den periodischen Zinssatz zu erhalten (in diesem Fall

0, 05 4 = 0, 0125

${frac{0,05}{4}}=0,0125$ ) und lösen Sie das Ziel

n * T

$n*t$ welches gerade hier

4 * 1

$4*1$ ist. Daraus ergibt sich folgende Gleichung:

ein = 1000 (1 + (0, 0125)) 4

$A=1000(1+(0,0125))^{{4}}$ .

Dies wird weiter vereinfacht, indem man nach dem Term in den Klammern auflöst,

1 + 0, 0125 = 1, 0125

$1+0,0125=1,0125$ . Die Gleichung sieht jetzt so aus:

ein = 1000 (1, 0125) 4

$A=1000(1.0125)^{{4}}$ .

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 5

5. Löse die Gleichung. Lösen Sie dann nach dem Exponenten auf, indem Sie den letzten Schritt mit vier potenzieren (d. h

1, 0125 * 1, 0125 * 1, 0125 * 1, 0125

$1.0125*1.0125*1.0125*1.0125$ ). Das liefert

1, 051

$1.051$ als Ergebnis auf. Die Gleichung lautet nun:

ein = 1000 (1, 051)

$A=1000(1.051)$ . Multiplizieren Sie diese beiden Zahlen und Sie erhalten

ein = 1051

$A=1051$ . Dies ist der Wert Ihres Kontos mit 5% Zinsen (aufgezinst pro Quartal) nach einem Jahr.

Beachten Sie, dass dies etwas höher ist als

1000 * 5 %

$1000*5%$ , die Sie bei der Einreichung des Jahreszinses vielleicht erwartet haben. Dies zeigt, wie wichtig es ist zu verstehen, wie und wann Ihr Interesse gebündelt ist!

Der Zins ist die Differenz zwischen A und P, also beträgt der gesamte verdiente Zinseszins

= 1051 - 1000 = 51

$=1051-1000=51$ .

Methode 2 von 3: Zinsen mit periodischen Beiträgen berechnen

Bildtitel Calculate Bank Interest on Savings Step 6

1. Verwenden Sie zuerst die Formel für akkumulierte Zinsen. Sie können auch Zinsen auf ein Konto berechnen, auf das Sie regelmäßige monatliche Beiträge überweisen. Dies ist nützlich, wenn Sie jeden Monat einen bestimmten Betrag sparen und dieses Geld auf Ihr Sparkonto legen. Die vollständige Gleichung lautet wie folgt:

ein = P (1 + (\frac{R}{n}))^{n T} + P m T * (1 + \frac{R}{n})^{n T} - 1 \frac{R}{n}

$A=P(1+({frac{r}{n}}))^{{nt}}+PMT*{frac{(1+{frac{r}{n}})^{{nt }}-1}{{frac{r}{n}}}}$

Ein einfacher Ansatz besteht darin, den Zinseszins auf den Kapitalbetrag von den Zinsen auf die monatlichen Beiträge (oder Zahlungen/PMT) zu trennen. Um zu beginnen, berechnen Sie zuerst die Zinsen auf das Kapital oder den Kapitalbetrag mithilfe der Formel für das angesammelte Sparen.
Wie mit dieser Formel beschrieben, können Sie die Verzinsung Ihres Sparkontos mit wiederkehrenden monatlichen Einlagen und Zinseszinsen täglich, monatlich oder vierteljährlich berechnen.

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 7

2. Verwenden Sie den zweiten Teil der Formel, um die Zinsen auf Ihre Einlagen zu berechnen. (PMT) steht für den Betrag Ihrer monatlichen Einzahlung.

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 8

3. Bestimmen Sie Ihre Variablen. Überprüfen Sie Ihr Konto oder Ihren Anlagevertrag, um die folgenden Variablen zu finden: Kapital `P`, der Jahreszins `r` und die Anzahl der Raten pro Jahr `n`. Wenn diese Variablen nicht ohne weiteres verfügbar sind, wenden Sie sich bitte an Ihre Bank, um diese Informationen anzufordern. Die Variable `t` steht für die Anzahl der zu berechnenden Jahre (oder Teile davon) und `PMT` steht für die Zahlung/den Beitrag pro Monat. Der Wert `A` stellt den Gesamtwert des Kontos nach einem Zeitraum und Einzahlungen Ihrer Wahl dar.

Das Kapital `P` stellt den Kontostand an dem Tag dar, an dem Sie mit der Berechnung beginnen.

Der Zinssatz `r` stellt die Zinsen dar, die jedes Jahr auf das Konto gezahlt werden. Es muss als Dezimalzahl in der Gleichung ausgedrückt werden. Das heißt, ein Zinssatz von 3% wird als 0,03 . angegeben. Sie erhalten diese Zahl, indem Sie den angegebenen Prozentsatz durch 100 . teilen.

Der Wert `n` gibt an, wie oft die Zinsen jährlich aufgezinst werden. Dies sind 365 mit einem täglichen, 12 monatlichen und 4 mit einem Zinseszins pro Quartal.

Der Wert für `t` stellt die Anzahl der Jahre dar, über die Sie die zukünftigen Zinsen berechnen. Dies ist die Anzahl der Jahre oder der Teil eines Jahres, wenn Sie weniger als ein Jahr annehmen (z. 0,0833 (1/12) für einen Monat).

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 9

4. Setze deine Werte in die Formel ein. Am Beispiel von P=1000, r=0,05 (5%), n=12 (monatlich zusammengestellt), t=3 Jahre und PMT=100 erhalten wir die folgende Gleichung:

ein = 1000 (1 + (0, 05 12))^{12 * 3} + 100 * (1 + 0, 05 12)^{12 * 3} - 1 \frac{0, 05}{12}

$A=1000(1+({frac{0,05}{12}}))^{{12*3}}+100*{frac{(1+{frac{0,05}{12} })^{ {12*3}}-1}{{frac{0.05}{12}}}}$

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 10

5. Vereinfachen Sie die Gleichung. Vereinfachen Sie das Ziel

\frac{R}{n}

${frac{r}{n}}$ wenn möglich durch Division des Zinssatzes, 0,05, durch 12. Das ist vereinfacht

ein = 1000 (1 + (0, 00417)) 12 * 3 + 100 * (1 + 0, 00417) 12 * 3 - 1 0, 00417

$A=1000(1+(0,00417))^{{12*3}}+100*{frac{(1+0,00417)^{{12*3}}-1}{0,00417} }$ Sie können auch vereinfachen, indem Sie einen zum Zinssatz in den Klammern hinzufügen. Die Gleichung sieht jetzt so aus:

ein = 1000 (1, 00417)) 12 * 3 + 100 * (1, 00417) 12 * 3 - 1 0, 00417

$A=1000(1.00417))^{{12*3}}+100*{frac{(1.00417)^{{12*3}}-1}{0.00417}}$

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 11

6. Löse die Exponenten. Lösen Sie zuerst die Terme innerhalb der Exponenten,

n * T

$n*t$ , daher

12 * 3 = 36

$12*3=36$ . Dann löse nach den Exponenten auf, um die Gleichung zu vereinfachen zu

ein = 1000 (1, 1616) + 100 * 1, 1616 - 1 0, 00417

$A=1000(1,1616)+100*{frac{1,1616-1}{0,00417}}$ Vereinfachen Sie, indem Sie eins subtrahieren und Sie erhalten

ein = 1000 (1, 1616) + 100 * 0, 1616 0, 00417

$A=1000(1,1616)+100*{frac{0,1616}{0,00417}}$

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 12

7. Führe die abschließenden Berechnungen durch. Multiplizieren Sie den ersten Teil der Gleichung und Sie erhalten $1.616. Lösen Sie den zweiten Teil der Gleichung, indem Sie zuerst den Zähler durch den Nenner des Bruchs dividieren, und Sie erhalten

0, 1616 0, 00417 = 38, 753

${frac{0,1616}{0,00417}}=38,753$ . Multiplizieren Sie diese Zahl mit dem Wert der Einzahlung (in diesem Fall 100 USD), um den zweiten Teil der Gleichung zu erhalten. Die Gleichung lautet nun:

ein = 1616 + 3875, 30 = 5491, 30

$A=1616+3875,30=5491,30$ . Der Kontostand ist unter diesen Umständen jetzt

5491, 30

$5491.30$ .

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 13

8. Berechnen Sie Ihre gesamten verdienten Zinsen. In dieser Gleichung sind die tatsächlichen Zinsen der Gesamtbetrag (A) abzüglich des Kapitals (P) und die Anzahl der Zahlungen multipliziert mit der Einzahlung (PMT*n*t). Also im Beispiel:

ich n T e R e S T = 5491, 30 - 1000 - 100 (12 * 3)

$Zinsen=5491,30-1000-100(12*3)$ und danach

5491, 30 - 1000 - 3600 = 891, 30

$5491,30-1000-3600=891,30$ .

Methode 3 von 3: Verwenden eines Arbeitsblatts zur Berechnung des Zinseszinses

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 14

1. Öffne ein neues Arbeitsblatt. Excel und ähnliche Tabellenkalkulationsprogramme (z. B. Google Sheets) können Ihnen bei diesen Berechnungen Zeit sparen und sogar Verknüpfungen in Form von integrierten Finanzfunktionen bereitstellen, um den Zinseszins zu berechnen.

Bildtitel Calculate Bank Interest on Savings Step 15

2. Benennen Sie Ihre Variablen. Bei der Verwendung eines Arbeitsblattes ist es immer hilfreich, so organisiert und übersichtlich wie möglich zu sein. Benennen Sie zunächst eine Zellenspalte mit den wichtigen Informationen, die Sie in Ihrer Berechnung verwenden (z. Zinsen, Kapital, Zeit, n, Einlagen).

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 16

3. Geben Sie Ihre Variablen ein. Geben Sie nun die Informationen zu Ihrem spezifischen Konto in die nächste Spalte ein. Dies erleichtert nicht nur das spätere Lesen und Interpretieren des Arbeitsblatts, sondern lässt Ihnen auch Raum, eine oder mehrere der Variablen zu einem späteren Zeitpunkt zu ändern, um verschiedene mögliche Einsparszenarien zu betrachten.

Bildtitel Berechnen Bankzinsen auf Spareinlagen Schritt 17

4. Stelle deine Gleichung auf. Der nächste Schritt besteht darin, Ihre eigene Version der Gleichung für aufgelaufene Zinsen einzugeben (

ein = P (1 + (\frac{R}{n}))^{n * T}

$A=P(1+({frac{r}{n}}))^{{n*t}}$ ) oder die erweiterte Version, die Ihre regelmäßigen monatlichen Einzahlungen berücksichtigt (

ein = P (1 + (\frac{R}{n}))^{n T} + P m T * (1 + \frac{R}{n})^{n T} - 1 \frac{R}{n}

$A=P(1+({frac{r}{n}}))^{{nt}}+PMT*{frac{(1+{frac{r}{n}})^{{nt }}-1}{{frac{r}{n}}}}$ ). Verwenden Sie eine beliebige leere Zelle, beginnen Sie mit einem `=` und verwenden Sie normale mathematische Konventionen (ggf. Klammern), um die richtige Gleichung einzugeben. Anstatt Variablen wie (P) und (n) einzugeben, geben Sie die entsprechenden Namen der Zelle ein, in der Sie die Datenwerte gespeichert haben, oder klicken Sie einfach auf die gewünschte Zelle, während Sie Ihre Gleichung bearbeiten.

Bildtitel Calculate Bank Interest on Savings Step 18

5. Finanzfunktionen nutzen. Excel bietet auch bestimmte Finanzfunktionen, die Ihnen bei Ihrer Berechnung helfen können. Besonders `Future Value` (TW) kann verwendet werden, da es den Wert eines Kontos zu einem bestimmten Zeitpunkt in der Zukunft berechnet, wobei die gleichen Variablen gegeben sind, an die Sie sich inzwischen gewöhnt haben. Um auf diese Funktion zuzugreifen, gehen Sie in eine leere Zelle und geben Sie `=TW(`. Excel zeigt dann ein Hilfefeld an, sobald Sie die Funktionsklammer öffnen, um Ihnen bei der Eingabe der richtigen Parameter für die Funktion zu helfen.

Die Funktion "Zukunftswert" dient dazu, einen Kontostand im Voraus zu begleichen, wenn sich die Zinsen weiter ansammeln, und nicht mit aufgelaufenen Sparzinsen. Als Ergebnis gibt es automatisch eine negative Zahl zurück. Sie können diesem Problem begegnen, indem Sie Folgendes eingeben:

= - 1 * T W (

$=-1*TW($

Die TW-Funktion verwendet ähnliche Datenparameter, durch Kommas getrennt, aber nicht genau gleich. Zum Beispiel: `Interesse` bezieht sich auf

R / n

$r/n$ (der jährliche Zinssatz geteilt durch `n`). Dadurch werden automatisch die Terme in Klammern der TW-Funktion berechnet.

Der Parameter `Zahl der Raten` bezieht sich auf die Variable

n * T

$n*t$ die Gesamtzahl der Raten, über die die Kumulierung berechnet wird und die Gesamtzahl der Zahlungen. Mit anderen Worten, wenn Ihr PMT nicht 0 ist, geht die VA-Funktion davon aus, dass Sie den PMT-Betrag über jeden Zeitraum addieren, wie durch "Zahl-Raten" definiert.

Beachten Sie, dass diese Funktion normalerweise verwendet wird, um (etwa) zu berechnen, wie sich der Kapitalbetrag einer Hypothek im Laufe der Zeit durch regelmäßige Zahlungen abbezahlt hat. Wenn Sie beispielsweise planen, fünf Jahre lang jeden Monat zu zahlen, wird die "Anzahl der Raten" zu 60 (5 Jahre x 12 Monate).

„Wette“ ist Ihr regelmäßiger Beitrag während des gesamten Zeitraums (ein Beitrag pro „n“)

`[hw]` (aktueller Wert) ist das Kapital - der Eröffnungssaldo Ihres Kontos.

Die letzte Variable `[type_number]` kann für diese Berechnung leer gelassen werden (in diesem Fall setzt die Funktion sie automatisch auf 0).

Die TW-Funktion bietet die Möglichkeit, einige grundlegende Berechnungen innerhalb der Funktionsparameter durchzuführen, zum Beispiel könnte die vollständig ausgefüllte Funktion TW so aussehen:

- 1 * T W (.05 / 12, 12, 100, 5000)

$-1*TW(.05/12,12,100,5000)$ . Dies bedeutet einen jährlichen Zinssatz von 5%, der monatlich für 12 Monate aufgezinst wird. Über diesen Zeitraum zahlen Sie 100 USD/Monat mit einem Eröffnungssaldo (Hauptbetrag) von 5.000 USD ein. Die Antwort auf diese Funktion gibt Ihnen den Kontostand nach 1 Jahr (6483,70 €).

Tipps

Es ist auch möglich, wenn auch komplizierter, den Zinseszins auf einem Konto mit unregelmäßigen Zahlungen zu berechnen. Bei dieser Methode wird die Verzinsung jeder Zahlung/Beitrag separat berechnet (mit der gleichen Gleichung wie oben beschrieben) und wird am besten mit einem Arbeitsblatt erreicht, um die Berechnung zu erleichtern.
Sie können auch einen kostenlosen Online-Jahreszinsrechner verwenden, um die Zinsen auf Ihrem Sparkonto zu ermitteln. Suchen Sie im Internet nach "Jahreszinsrechner" oder "Jahreszinsrechner", um eine Liste von Websites zu erhalten, die diesen Service kostenlos anbieten.