Berechnen der Fibonacci-Folge (mit Bildern)

Schritte
- Methode 1 von 2: Verwenden Sie eine Tabelle
- Methode 2 von 2: Verwenden der Binet-Formel und des Goldenen Mittels

Die Fibonacci-Folge ist eine Zahlenfolge, die durch Addieren der beiden vorherigen Zahlen in der Folge erzeugt wird. Die Zahlen der Serie sind häufig in der Natur und in der Kunst zu sehen, wie etwa Spiralen und der Goldene Schnitt. Der einfachste Weg, die Reihe zu berechnen, besteht darin, eine Tabelle zu erstellen; Dies ist jedoch nicht praktikabel, wenn Sie beispielsweise nach dem 100. Term in der Sequenz suchen. In diesem Fall verwenden Sie die Binet-Formel.

Schritte

Methode 1 von 2: Verwenden Sie eine Tabelle

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 1

1. Erstellen Sie eine Tabelle mit zwei Spalten. Die Anzahl der Zeilen hängt von der Anzahl der Zahlen in der Fibonacci-Folge ab, die Sie berechnen möchten.

Wenn Sie beispielsweise die fünfte Zahl in der Folge finden möchten, hat Ihre Tabelle fünf Zeilen.
Mit dieser Tabellenmethode ist es nicht möglich, eine Zahl weiter unten in der Folge zu finden, ohne zuerst alle Zahlen davor zu berechnen. Wenn Sie beispielsweise die 100. Zahl in der Folge finden möchten, müssen Sie zuerst die ersten 99 Zahlen finden. Daher funktioniert die Tabellenmethode nur für Zahlen am Anfang der Folge.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 2

2. Geben Sie die Zahlenfolge in die linke Spalte ein. Dies bedeutet, dass Sie eine Folge fortlaufender Ordnungszahlen eingeben, beginnend mit "1."

Der Begriff bezieht sich auf die Position der Zahl in der Fibonacci-Folge.

Wenn Sie beispielsweise die fünfte Zahl in der Folge berechnen möchten, schreiben Sie die 1., 2., 3., 4., 5. in die linke Spalte. Dies wird Ihnen helfen, die ersten fünf Terme der Sequenz zu identifizieren.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 3

3. Setze 1 in die erste Zeile der rechten Spalte. Dies ist der Ausgangspunkt der Fibonacci-Folge. Mit anderen Worten, der erste Term in der Folge ist 1.

Die korrekte Fibonacci-Folge beginnt immer mit 1. Wenn Sie mit einer anderen Zahl beginnen möchten, finden Sie nicht das richtige Muster der Fibonacci-Folge.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 4

4. Zähle den ersten Term (1) und 0. zusammen auf. Dadurch erhältst du die zweite Zahl in der Folge.

Denken Sie daran, dass Sie nur die beiden vorherigen Zahlen addieren müssen, um eine bestimmte Zahl der Fibonacci-Folge zu finden.

Um die Sequenz zu erstellen, kommt 0 vor 1 (dem ersten Term), also: 1 + 0 = 1.

Bild mit dem Titel Berechnen Sie die Fibonacci-Folge Schritt 5

5. Addiere den ersten Term (1) und den zweiten Term (1) zusammen. Dadurch erhältst du die dritte Zahl in der Folge.

1 + 1 = 2. Der dritte Term ist 2.

Bild mit dem Titel Berechnen Sie die Fibonacci-Folge Schritt 6

6. Addiere den zweiten Term (1) und den dritten Term (2) zusammen, um die vierte Zahl in der Folge zu erhalten.

1 + 2 = 3. Der vierte Term ist 3.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 7

7. Addiere den dritten Term (2) und den vierten Term (3) zusammen. Jetzt kennst du die fünfte Zahl in der Folge.

2 + 3 = 5. Der fünfte Term ist 5.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 8

8. Addiere die beiden vorherigen Zahlen zusammen, um eine beliebige Zahl in der Fibonacci-Folge zu finden. Wenn Sie diese Methode verwenden, verwenden Sie die Formel

F n = F_{n - 1} + F_{n - 2}

$F_{{n}}=F_{{n-1}}+F_{{n-2}}$ . Da dies keine geschlossene Formel ist, können Sie nicht jeden Term in der Reihe berechnen, ohne zuerst alle vorhergehenden Zahlen zu berechnen.

Methode 2 von 2: Verwenden der Binet-Formel und des Goldenen Mittels

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 9

1. Schreiben Sie die Formel auf:

x n

$x_{{n}}$ =

φ n - (1 - φ)^{n} \sqrt{5}

${frac{phi^{{n}}-(1-phi)^{{n}}}{{sqrt{5}}}}$ . In der Formel,

x n

$x_{{n}}$ = der Begriff in der Sequenz, die Sie suchen möchten,

n

$n$ = die Positionsnummer des Termes in der Reihe, und

φ

$phi$ = der goldene Schnitt.

Dies ist eine geschlossene Formel, sodass Sie einen bestimmten Term in der Reihe berechnen können, ohne alle vorherigen berechnen zu müssen.
Diese Formel ist eine vereinfachte Formel, die von der Fibonacci-Formel von Binet abgeleitet ist.
Die Formel wendet den Goldenen Schnitt an ( $φ$ $phi$ ), da das Verhältnis zweier aufeinanderfolgender Zahlen in der Fibonacci-Folge dem Goldenen Schnitt sehr ähnlich ist.

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 10

2. Passen Sie die Zahl für an n{displaystyle n} $n$ auf die Formel anwenden. Der

n

$n$ steht für den gesuchten Begriff in der Sequenz.

Wenn Sie beispielsweise nach der fünften Zahl in der Folge suchen, geben Sie 5 . ein. Ihre Formel sollte nun so aussehen:

x 5

$x_{{5}}$ =

φ 5 - (1 - φ)^{5} \sqrt{5}

${frac{phi^{{5}}-(1-phi)^{{5}}}{{sqrt{5}}}}$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 11

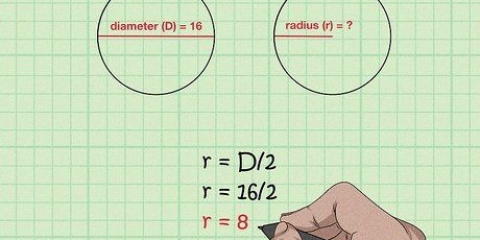
3. Ersetzen Sie den Goldenen Schnitt in der Formel. Verwenden Sie 1,618034 als Näherung für den Goldenen Schnitt.

Wenn Sie beispielsweise nach der fünften Zahl in der Folge suchen, sieht die eingegebene Formel wie folgt aus:

x 5

$x_{{5}}$ =

(1, 618034) 5 - (1 - 1, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(1-1,618034)^{{5}}}{{sqrt{5}}}}$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 12

4. Vervollständigen Sie die Berechnungen in Klammern. Betrachten Sie die Reihenfolge der arithmetischen Operationen, indem Sie zuerst den Teil in Klammern berechnen:

1 - 1, 618034 = - 0, 618034

$1-1.618034=-0.618034$ .

Im Beispiel wird die Gleichung

x 5

$x_{{5}}$ =

(1, 618034) 5 - (- 0, 618034)^{5} \sqrt{5}

${frac{(1.618034)^{{5}}-(-0.618034)^{{5}}}{{sqrt{5}}}}$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 13

5. Berechnen Sie die Exponenten. Multiplizieren Sie die beiden Zahlen in Klammern im Zähler mit dem entsprechenden Exponenten.

Im Beispiel,

1, 618034 5 = 11, 090170

$1,618034^{{5}}=11.090170$ ;

- 0, 618034 5 = - 0, 090169

$-0.618034^{{5}}=-0.090169$ . Die Gleichung wird also

x 5 = 11, 090170 - (- 0, 090169) \sqrt{5}

$x_{{5}}={frac{11,090170-(-0,090169)}{{sqrt{5}}}}$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 14

6. Vervollständigen Sie die Berechnung. Bevor Sie mit dem Dividieren fortfahren, müssen Sie zuerst die beiden Zahlen im Zähler subtrahieren.

Im Beispiel,

11, 090170 - (- 0, 090169) = 11, 180339

$11.090170-(-0.090169)=11.180339$ , also wird die Gleichung

x 5

$x_{{5}}$ =

11, 180339 \sqrt{5}

${frac{11,180339}{{sqrt{5}}}}$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 15

7. Dividiere durch die Quadratwurzel von fünf. Die Quadratwurzel aus fünf wird auf 2,236067 . gerundet.

In der Beispielaufgabe,

11, 180339 2, 236067 = 5, 000002

${frac{11,180339}{2,236067}}=5.000002$ .

Bildtitel Berechnen Sie die Fibonacci-Folge Schritt 16

8. Auf die nächste ganze Zahl runden. Ihre Antwort ist eine Dezimalzahl, kommt aber einer ganzen Zahl sehr nahe. Diese ganze Zahl repräsentiert die Zahl in der Fibonacci-Folge.

Wenn Sie den vollen Goldenen Schnitt verwendet und nichts gerundet haben, erhalten Sie eine ganze Zahl. Es ist jedoch praktischer zu runden, was zu einer Dezimalzahl führt.

Im Beispiel beträgt Ihre mit einem Taschenrechner berechnete Antwort ungefähr 5.000002. Auf die nächste ganze Zahl gerundet, lautet Ihre Antwort fünf, was auch die fünfte Zahl in der Fibonacci-Folge ist.