Nehmen wir in unserem Beispiel an, dass die Masse von 10 kg an einem Seil hängt, das nicht an einem Balken befestigt ist, sondern dazu dient, die Masse mit einer Beschleunigung von 1 m/s . nach oben zu heben. In solchen Fällen müssen wir neben der Beschleunigung auf die Masse auch die Gravitationskraft berücksichtigen, indem wir diese wie folgt lösen: FT = Fg + m × a FT = 98 + 10 kg × 1 m/s FT = 108 Newton. 
Da sich Richtung und Größe der Zentripetalkraft mit der Bewegung des Objekts auf dem Seil und der Geschwindigkeit ändert, ändert sich auch die Gesamtspannung im Seil, das immer parallel zum Seil zum Mittelpunkt zieht. Denken Sie daran, dass die Gravitationskonstante das Objekt anzieht. Wenn also ein Objekt in vertikaler Position herumgeworfen wird, ist die Gesamtspannung die größten am unteren Rand der Bewegungsbahn des Objekts (bei einer Pendeluhr wird dies auch als Gleichgewicht bezeichnet), wo sich das Objekt am schnellsten bewegt. Die Spannung ist am oberen Rand der Kreisbewegung am geringsten, wo die Geschwindigkeit am niedrigsten ist. Nehmen wir im Beispiel an, dass das Objekt wie ein Pendel schwingt. Das Seil ist 1,5 Meter lang und die Masse bewegt sich am tiefsten Punkt mit einer Geschwindigkeit von 2 m/s. Wenn wir die Spannung an diesem Punkt berechnen wollen, dem Punkt, an dem die Geschwindigkeit am höchsten ist, müssen wir zuerst sehen, dass die Schwerkraftspannung an diesem Punkt dieselbe ist wie bei der Ruhe des Pendels - 98 Newton. Um die Zentripetalkraft zu ermitteln, berechnen wir wie folgt: FC = m × f/r FC = 10 × 2/1.5 FC =10 × 2,67 = 26,7 Newton. Die Gesamtspannung beträgt also 98 + 26,7 = 124,7 Newton. 
Die Aufteilung der Schwerkraft in zwei Vektoren könnte Ihnen helfen, dieses Konzept zu visualisieren. An jedem Punkt im Bewegungsbogen eines schwingenden Objekts bildet das Seil einen Winkel von "θ" mit der Linie durch das Gleichgewicht und dem Mittelpunkt der Drehung. Während das Seil schwingt, kann man die Schwerkraft (m × g) in 2 Vektoren aufteilen - mgsin(θ) ist die Tangente an den Bogen in Richtung des Gleichgewichts und mgcos(θ), die Parallele zur Zugkraft im entgegengesetzten Richtung. Die Spannung muss nur mgcos(θ) entgegensetzen – der Kraft, die entgegenwirkt – nicht der vollen Schwerkraft (außer am Gleichgewichtspunkt, wenn sie gleich der Spannung ist). Angenommen, das Pendel bildet mit der Vertikalen einen Winkel von 15 Grad und hat dann eine Geschwindigkeit von 1,5 m/s. Wir ermitteln die Spannung wie folgt: Belastung durch Schwerkraft (Tg) = 98cos(15) = 98(0,96) = 94,08 Newton Zentripetalkraft (FC) = 10 × 1,5/1,5 = 10 × 1,5 = 15 Newton Gesamtspannung = Tg + FC = 94,08 + 15 = 109,08 Newton. 
Angenommen, die 10 kg Masse schwingt nicht mehr, sondern wird horizontal am Boden und an einem Seil mitgeschleppt. Nun sagen wir, dass der Boden einen Gleitreibungskoeffizienten von 0,5 hat und sich die Masse mit konstanter Geschwindigkeit bewegt, aber wir wollen ihn mit 1 m/s . beschleunigen. Diese neue Zuordnung zeigt zwei wichtige Änderungen: Zum einen müssen wir die Schwerkraftspannung nicht mehr berechnen, da das Seil die Masse nicht mehr trägt und der Kraft entgegenwirkt. Wir müssen nun die Reibungskraft und die daraus resultierende Spannung sowie die Spannung durch die Beschleunigung des Objekts berücksichtigen. Wir lösen das wie folgt: Normalkraft (N) = 10 kg × 9.8 (Erdbeschleunigung) = 98 N Gleitreibungskraft (FR) = 0.5 × 98 N = 49 Newton Beschleunigungskraft (Fein) = 10 kg × 1 m/s = 10 Newton Gesamtspannung = FR + Fein = 49 + 10 = 59 Newton. 
Angenommen, wir haben ein System mit einer Masse von 10 kg (m1), vertikal verbunden über eine Umlenkrolle, mit einer Masse von 5 kg (m2) auf einer 60-Grad-Neigung (wir gehen davon aus, dass die Neigung reibungslos ist). Um die Spannung im Seil zu finden, ist es einfacher, als Erster Gleichungen für die Kräfte zu formulieren, die die Massen beschleunigen. Gehen Sie wie folgt vor: Die hängende Masse ist schwerer und wir müssen keine Reibung berücksichtigen, also wissen wir, dass es eine Beschleunigung nach unten gibt. Da aber die Spannung im Seil die Masse nach oben zieht, berechnen wir die Nettokraft auf das Seil wie folgt: F = m1(g) - T oder 10(9.8) - T = 98 - T. Wir wissen, dass die Masse den Hang hinauf beschleunigen wird. Da der Hang reibungsfrei ist, wissen wir, dass die Spannung die Masse den Hang hinaufzieht, nur durch die Eigenmasse des Gewichts zurückgehalten. Die Kraftkomponente, die das Gewicht nach unten zieht, wird mit mgsin(θ) berechnet. In unserem Fall können wir also sagen, dass das Gewicht den Hang bergauf um die Nettokraft F = T - m . beschleunigt2(g)sünde(60) = T - 5(9.8)(.87) = T - 42.63. Die Beschleunigung der beiden Massen ist gleich, also haben wir (98 - T)/m1 = T - 42.63 /m2. Nach etwas einfacher Algebra erhalten wir T = 61.09 Newton. 
Angenommen in diesem Y-förmigen System hat das Objekt ein Gewicht von 10 kg und die beiden oberen Seile bilden mit der Decke einen Winkel von 30 Grad und 60 Grad. Wenn wir die Spannung in jedem der oberen Seile finden wollen, müssen wir die vertikalen und horizontalen Komponenten der Spannung für jedes Seil berücksichtigen. Die beiden Seile in diesem Beispiel hängen senkrecht zueinander, sodass diese Spannungen gemäß den Definitionen der trigonometrischen Funktionen leicht berechnet werden können. Also wie folgt: Das Verhältnis zwischen T1 oder T2 und T = m(g) ist gleich dem Sinus des Winkels zwischen jedem Tragseil und der Decke. für T1 ist sin(30) = 0.5, während für T2 gilt sin(60) = 0,87. Multiplizieren Sie die Spannung im unteren Seil (T = mg) mit dem Sinus jedes Winkels, um T . zu erhalten1 und T2 finden. T1 =0,5 × m(g) =0,5 × 10(9,8) = 49 Newton. T2 =0,87 × m(g) =0,87 × 10(9,8) = 85,26 Newton.
Berechnung von kräften in der physik
In der Physik ist Spannung die Kraft, die von einem Seil, einer Schnur, einem Kabel oder einem ähnlichen Objekt auf ein oder mehrere andere Objekte ausgeübt wird. Alles, was gezogen wird, wird aufgehängt, gestützt oder an einem Seil befestigt.D. schwingt, ist der Zugkraft ausgesetzt. Wie andere Kräfte kann auch Spannung Gegenstände beschleunigen oder verformen. Spannung berechnen zu können ist eine wichtige Fähigkeit für Physikstudenten, aber auch für Ingenieure und Architekten. Denn um sichere Gebäude zu gestalten, müssen sie genau wissen, ob die Spannung eines Seils der Belastung eines Gegenstandes standhält. Lesen Sie bei Schritt 1 weiter, um zu erfahren, wie Sie Stress in verschiedenen physikalischen Systemen berechnen.
Schritte
Methode 1 von 2: Ermitteln der Spannung an einer einzelnen Schnur

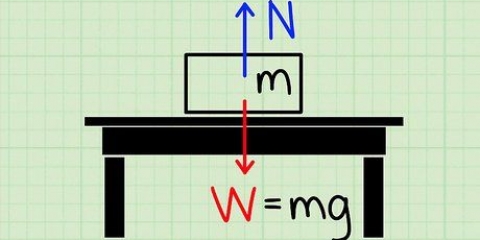
1. Bestimmen Sie die Kräfte auf jeder Seite des Drahtes. Die Spannung in einem bestimmten Strang eines Seils ist die Summe aller Kräfte, die das Seil von beiden Enden ziehen. Vergessen Sie nicht: Kraft = Masse × Beschleunigung. Angenommen, das Seil ist stark gespannt, dann führt jede Änderung der Beschleunigung oder Masse der Gegenstände, die das Seil unterstützt, zu einer Änderung der Spannung im Seil. Vergiss die Konstante Beschleunigung aufgrund der Schwerkraft auch nicht – selbst im ruhenden System ist jede Komponente der Schwerkraft ausgesetzt. Die Spannung in einem bestimmten Seil kann ausgedrückt werden als T = (m × g) + (m × a), wobei "g" die Beschleunigung ist auf die Schwerkraft eines vom Seil gestützten Objekts zurückzuführen, und "ein" ist jede andere Beschleunigung auf ein beliebiges Objekt, das vom Seil getragen wird.
- Der Einfachheit halber können wir annehmen, dass es sich um aidealer Faden – mit anderen Worten, dass das Seil, das Kabel usw. ist dünn und masselos und kann sich nicht dehnen oder brechen.
- Ein Beispiel: Angenommen, wir haben ein System, bei dem eine Masse an einem Holzbalken hängt, befestigt mit einem einzigen Seil (siehe Bild). Immer noch bewegen die Massen das Seil – das ganze System ruht. Wir wissen jetzt, dass die Masse im Gleichgewicht ist, wobei die Zugkraft gleich der Gravitationskraft auf die Masse ist. Mit anderen Worten, Spannung (FT) = Kraft oder Schwerkraft (Fg) = m × g.
- Angenommen wir haben eine Masse von 10 kg, dann gilt: Zug = 10 kg × 9,8 m/s = 98 Newton.

2. Achte auf die Beschleunigung. Die Schwerkraft ist nicht die einzige Kraft, die die Spannung in einem Seil beeinflusst - jede Kraft kann mit der Beschleunigung eines Objekts in Verbindung gebracht werden, mit dem das Seil verbunden ist. Wird ein hängender Gegenstand durch eine Kraft auf das Seil oder Seil beschleunigt, dann addiert sich die durch die Beschleunigung verursachte Kraft (Masse × Beschleunigung) zu der durch die Masse des Gegenstandes verursachten Spannung.

3. Berücksichtigen Sie auch ein kreisförmiges Zahnrad. Ein um einen Mittelpunkt eines Seils gedrehter Gegenstand (z. B. ein Pendel) übt durch die Zentripetalkraft eine Spannung auf das Seil aus. Zentripetalkraft ist die Kraft, die das Seil auf ein Objekt ausübt, indem es es nach innen zieht "Ziehen", damit sich das Objekt weiterhin in einem Bogen bewegt, anstatt geradeaus zu gehen. Je schneller sich das Objekt bewegt, desto größer ist die Zentripetalkraft. Zentripetalkraft (FC) ist gleich m × v/r wobei "m" ist gleich der Masse, "v" ist die Geschwindigkeit und "R" ist der Radius des Kreises, d. h. die Bahn, auf der sich das Objekt bewegt.

4. Verstehen Sie, dass sich die Spannung während der Pendelphase aufgrund der Schwerkraft ändert. Wie bereits erwähnt, ändern sich sowohl die Richtung als auch die Größe der Zentripetalkraft, wenn ein Objekt schwingt. Aber obwohl die Schwerkraft konstant bleibt, Spannung durch Schwerkraft auch ändern. Wie ein schwingendes Objekt nicht Unterseite der Pendelschwingung (der Gleichgewichtspunkt), dann zieht die Schwerkraft gerade nach unten, aber die Spannung zieht das Objekt in einem Winkel. Aus diesem Grund wird die Spannung einen Teil der Gravitationskraft aufheben, aber nicht vollständig.

5. Denken Sie auch an die Reibung. Jeder Gegenstand, der durch ein Seil gezogen wird und von einem anderen Gegenstand (oder einer Flüssigkeit) Reibung erfährt, überträgt diese Reibungskraft auf die Spannung im Seil. Die Reibungskraft zwischen zwei Objekten wird wie in jeder anderen Situation berechnet – nach folgender Gleichung: Reibungskraft FR = (mu)N, wobei mu der Reibungskoeffizient zwischen den beiden Objekten ist und wobei N die Normalkraft zwischen den beiden Objekten ist (die Kraft, mit der sie gegeneinander drücken). Beachten Sie, dass die Haftreibung – die Reibung, die auftritt, wenn Sie versuchen, ein stationäres Objekt zu bewegen – sich von der Gleitreibung unterscheidet – der Reibung, die auftritt, wenn Sie versuchen, ein sich bewegendes Objekt in Bewegung zu halten.
Methode 2 von 2: Berechnung der Spannung bei mehreren Akkorden

1. Heben von parallelen vertikalen Lasten mit einer Umlenkrolle. Eine Seilrolle ist eine einfache Maschine, die aus einem aufgehängten Rad besteht, das es der Zugkraft in einem Seil ermöglicht, die Richtung zu ändern. In einem einfachen Aufbau läuft das Seil oder Kabel von einer hängenden Masse nach oben durch die Rolle, dann nach unten zu einer anderen Masse, wodurch Sie zwei Seillängen erhalten. Aber die Spannung in beiden Seilteilen ist gleich, auch wenn an beiden Seilenden unterschiedlich große Massen hängen. In einem System aus zwei an einer Rolle aufgehängten Massen beträgt die Spannung 2g(m1)(m2)/(m2+m1), wobei "g" die Beschleunigung ist auf die Schwerkraft zurückzuführen, "m1" die Masse von Objekt 1 und "m2" die Masse des Objekts 2. Beachten Sie, dass das System beschleunigt wird, da sich die Masse nach unten und die 5 kg nach oben bewegen, da eine Masse schwerer ist als die andere.
- Beachten Sie, dass wir a "ideale Riemenscheibe – keine Masse, keine Reibung und Riemenscheiben, die nicht brechen, sich verformen oder von der Decke lösen können.
- Angenommen, wir haben zwei Massen, die an einer Rolle hängen, an parallelen Seilen. Gewicht 1 hat eine Masse von 10 kg und Gewicht 2 hat eine Masse von 5 kg. In diesem Fall ermitteln wir die Spannung wie folgt:
- T = 2g(m1)(m2)/(m2+m1)
- T = 2(9,8)(10)(5)/(5 + 10)
- T = 19,6(50)/(15)
- T = 980/15
- T = 65,33 Newton.
2. Heben von Gewichten mit einer Rolle an senkrechten, aber nicht parallelen Seilen. Riemenscheiben werden oft verwendet, um Spannung in eine andere Richtung als nach oben oder unten zu bringen. Wenn beispielsweise an einem Ende des Seils eine Masse senkrecht hängt, während am anderen Ende eine zweite Masse an einem Hang festgebunden ist, hat dieses nicht parallele Flaschenzugsystem die Form eines Dreiecks, dessen Scheitel die erste Masse sind. die zweite Masse und die Riemenscheibe selbst. In diesem Fall wird die Spannung im Seil sowohl durch die Schwerkraft auf die Masse als auch durch die parallel zum Diagonalabschnitt des Seils wirkende Komponente der Zugkraft bestimmt.

3. Verwenden mehrerer Schnüre zum Aufhängen eines Objekts. Schließlich betrachten wir den Fall, dass ein Objekt an a . hängt "Y-förmig" Seilsystem – zwei Seile sind an der Decke befestigt und treffen sich in einem zentralen Punkt, an dem ein Gewicht an einem dritten Seil hängt. Die Spannung im dritten Seil ist offensichtlich – das ist einfach die resultierende Spannung aufgrund der Schwerkraft. Die Spannungen in den anderen beiden Seilen sind unterschiedlich und sollten, wenn sie zusammengezählt werden, nach oben und in vertikaler Richtung gleich der Schwerkraft und in horizontaler Richtung gleich Null sein (vorausgesetzt, das System ruht). Die Spannung in den Seilen wird durch die Masse des hängenden Gegenstands sowie den Winkel jedes Seils zur Decke beeinflusst.
"Berechnung von kräften in der physik"
Оцените, пожалуйста статью