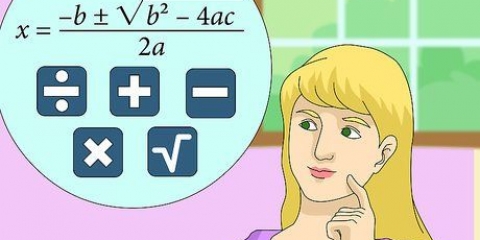Beispiel 1: Der Sinus von 30 Grad beträgt 0,50. Dies bedeutet, dass die gegenüberliegende Seite eines 30-Grad-Winkels genau die halbe Länge der Hypotenuse beträgt. Beispiel 2: Diese Beziehung kann verwendet werden, um die Länge der Hypotenuse in einem Dreieck mit einem Winkel von 30 Grad mit einer gegenüberliegenden Seite von 18 cm . zu bestimmen. Die Hypotenuse wäre dann 36 cm. 
Sinus (Sinus) Kosinus (Kos) Tangente (Bräune) Schnittlinie (Sek.) Kosekans (Csc) Kotangens (Kinderbett) Der Mond hat einen vorhersehbaren Zyklus von etwa 29,5 Tagen. Denken Sie daran, die Gezeiten an einem bestimmten Strand zu messen. Bei Flut erreicht es eine gewisse Höhe und sinkt dann zu Ebbe. Ab Ebbe steigt das Wasser am Strand höher, bis die Flut wieder da ist. Dieser Zyklus würde sich unbegrenzt fortsetzen und kann als trigonometrische Funktion wie ein Kosinus dargestellt werden. Schreibe auch alle Fragen auf, die du deinem Lehrer stellen möchtest. In den meisten Büchern stehen die Antworten für eine Reihe von Übungen ganz hinten. So können Sie Ihre Arbeit überprüfen. Wenn Ihr Lehrer es vorzieht, ohne Unterbrechungen zu unterrichten, stellen Sie Ihre Fragen vor oder nach dem Unterricht. Denken Sie daran, es ist die Aufgabe des Lehrers, Ihnen beim Erlernen der Trigonometrie zu helfen, also seien Sie nicht schüchtern.
Trigonometrie lernen
Trigonometrie ist der Zweig der Mathematik, der sich mit Dreiecken und Zyklen befasst. Trigonometrische Funktionen werden verwendet, um die Eigenschaften von Winkeln, die Beziehungen in einem Dreieck und die Graphen eines wiederkehrenden Zyklus zu beschreiben. Das Erlernen der Trigonometrie hilft, diese Beziehungen und Zyklen zu verstehen, zu visualisieren und darzustellen. Wenn Sie Selbststudium mit Aufmerksamkeit während des Unterrichts kombinieren, können Sie beginnen, die grundlegenden trigonometrischen Konzepte zu verstehen und wahrscheinlich Zyklen in der Welt um Sie herum zu bemerken.
Schritte
Methode 1 von 4: Konzentration auf wichtige trigonometrische Konzepte

1. Definiere die Teile eines Dreiecks. Im Kern ist die Trigonometrie das Studium der Beziehungen in Dreiecken. Ein Dreieck hat drei Seiten und drei Winkel. Definitionsgemäß beträgt die Winkelsumme eines Dreiecks 180 Grad. Sie müssen sich mit Dreiecken und Dreiecksterminologie vertraut machen, um die Trigonometrie gut zu beherrschen. Einige häufig verwendete Begriffe:
- Hypotenuse ― die längste Seite eines Dreiecks.
- Stumpfer Winkel ein Winkel von mehr als 90 Grad.
- Spitzer Winkel―Ein Winkel von weniger als 90 Grad.

2. Erfahren Sie, wie Sie den Einheitskreis bilden. Mit einem Einheitskreis kann man ein Dreieck so skalieren, dass die Hypotenuse gleich eins ist. Dies ist nützlich, da trigonometrische Funktionen wie Sinus und Cosinus in Prozent ausgedrückt werden können. Sobald Sie den Einheitskreis verstanden haben, können Sie die trigonometrischen Werte eines bestimmten Winkels verwenden, um Fragen zu Dreiecken mit diesen Winkeln zu beantworten.

3. Kennen Sie die trigonometrischen Funktionen. Es gibt sechs Funktionen, die für das Verständnis der Trigonometrie unerlässlich sind. Zusammen definieren sie die Beziehungen innerhalb eines Dreiecks und ermöglichen es Ihnen, die einzigartigen Eigenschaften eines Dreiecks zu verstehen. Diese sechs Funktionen sind:
4. Beziehungen verstehen. Eines der wichtigsten Dinge, die Sie bei trigonometrischen Funktionen verstehen müssen, ist, dass alle Funktionen miteinander verbunden sind. Während die Werte für Sinus, Cosinus, Tangens usw. alle haben ihre eigene Anwendung, sie sind am nützlichsten wegen der Beziehungen, die zwischen ihnen bestehen. Der Einheitskreis schränkt diese Zusammenhänge ein, damit sie leicht verständlich sind. Sobald Sie den Einheitskreis verstanden haben, können Sie die darin beschriebenen Beziehungen verwenden, um andere Probleme zu modellieren.
Methode 2 von 4: Die Anwendungen der Trigonometrie verstehen
1. Verstehen Sie die grundlegende wissenschaftliche Anwendung der Trigonometrie. Neben dem Studium trigonometrischer Funktionen, nur weil sie Trigonometrie mögen, werden diese Eigenschaften auch von Mathematikern und Wissenschaftlern praktisch angewendet. Trigonometrie kann verwendet werden, um Werte für Winkel oder Liniensegmente zu finden. Sie können zyklische Eigenschaften auch beschreiben, indem Sie sie als trigonometrische Funktionen zeichnen.
- Zum Beispiel kann die Bewegung einer Schraubenfeder mit einem Graphen als Sinuswelle beschrieben werden.
2. Denken Sie an die Kreisläufe in der Natur. Manchmal fällt es Menschen schwer, abstrakte Konzepte in Mathematik oder Naturwissenschaften zu verstehen. Wenn Sie feststellen, dass diese Konzepte in der Welt um Sie herum präsent sind, können Sie sie oft in einem neuen Licht betrachten. Suchen Sie nach Dingen in Ihrem Leben, die in Zyklen passieren, und versuchen Sie, sie mit der Trigonometrie in Verbindung zu bringen.
3. Visualisiere, wie man natürliche Zyklen studiert. Sobald Sie erkennen, dass die Natur voller Zyklen ist, können Sie darüber nachdenken, wie Sie diese Zyklen studieren könnten. Überlegen Sie, wie ein Diagramm dieser Zyklen aussehen würde. Aus der Grafik können Sie dann eine Gleichung zur Beschreibung des beobachteten Phänomens ableiten. Dies gibt trigonometrischen Funktionen eine Bedeutung, damit Sie ihre Nützlichkeit besser verstehen können.
Methode 3 von 4: Vorher studieren
1. Lesen Sie das Kapitel. Trigonometrische Konzepte sind für viele Menschen auf Anhieb schwer zu verstehen. Wenn Sie das Kapitel vor der Behandlung im Unterricht lesen, werden Sie mit dem Material vertrauter. Je öfter Sie das Material sehen, desto besser können Sie die verschiedenen Konzepte der Trigonometrie miteinander in Beziehung setzen.
- Damit kannst du vor dem Unterricht alle Konzepte durchgehen, mit denen du Schwierigkeiten hast.
2. Führe ein Notizbuch. In einem Buch zu blättern ist besser als nichts, aber es ist nicht die gründliche Lektüre, die Ihnen die Trigonometrie beibringt. Machen Sie sich detaillierte Notizen zu jedem Kapitel, das Sie lesen. Denken Sie daran, dass Trigonometrie kumulativ ist und die Konzepte aufeinander aufbauen, sodass Ihre Notizen aus den vorherigen Kapiteln Ihnen helfen können, das nächste Kapitel zu verstehen.
3. Mach die Übungen aus dem Buch. Manche Leute sind gut darin, Trigonometrie zu visualisieren, aber Sie müssen auch Übungen machen. Um sicherzustellen, dass Sie den Stoff wirklich verstehen, machen Sie vor dem Unterricht einige Übungen. So weißt du genau, wofür du im Unterricht Hilfe brauchst, wenn du Probleme mit etwas hast.
4. Bringen Sie Ihre Lernmaterialien mit zum Unterricht. Wenn Sie Ihre Notizen und Übungsübungen mit in den Unterricht bringen, erhalten Sie etwas, worauf Sie sich beziehen können. Dies frischt die Dinge auf, die Sie bereits verstanden haben, und weist Sie auf Konzepte hin, die besser erklärt werden müssen. Erhalten Sie Antworten auf alle Fragen, die Sie beim Lesen aufgeschrieben haben.
Methode 4 von 4: Notizen während des Unterrichts machen
1. Machen Sie sich Notizen im selben Notizbuch. Trigonometrische Konzepte hängen alle zusammen. Am besten bewahren Sie alle Ihre Notizen an einem Ort auf, damit Sie später darauf zurückgreifen können. Bestimmen Sie ein bestimmtes Notizbuch oder einen Ordner für Ihr Studium der Trigonometrie.
- Hier kannst du auch deine Übungsaufgaben machen.
2. Machen Sie die Trigonometrie zu Ihrer Priorität im Unterricht. Nutze deine Unterrichtszeit nicht zum Chatten oder Nachholen von Hausaufgaben aus einer anderen Klasse. Während des Trigonometrieunterrichts ist es wichtig, sich voll und ganz auf den Unterricht und die Aufgaben zu konzentrieren. Schreiben Sie die Notizen auf, die der Lehrer an die Tafel geschrieben oder als wichtig markiert hat.
3. Bleiben Sie im Klassenzimmer involviert. Melde dich freiwillig, um Probleme an der Tafel zu lösen oder teile deine Antworten auf Übungsprobleme. Stellen Sie Fragen, wenn Sie etwas nicht verstanden haben. Halte die Kommunikation so offen und flexibel wie möglich, soweit es dein Lehrer erlaubt. So wird das Lernen und die Freude an der Trigonometrie viel einfacher.
4. Dann mach mehr Übungsaufgaben. Machen Sie alle Hausaufgaben, die Sie bekommen haben. Hausaufgaben sind gute Indikatoren für Prüfungsfragen. Stellen Sie sicher, dass Sie jedes Problem verstanden haben Wenn Sie keine Hausaufgaben erhalten haben, bearbeiten Sie die Probleme aus dem Buch, die den Konzepten der letzten Lektion entsprechen.
Tipps
- Denken Sie daran, dass Mathematik eine Denkweise ist und nicht nur Formeln, an die Sie sich erinnern können.
- Erfahren Sie mehr über Algebra und Geometrie.
Warnungen
- Trigonometrie kann man nicht durch Stanzen lernen. Sie müssen die zugrunde liegenden Konzepte verstehen.
- Das Stempeln für einen Trigonometrietest funktioniert praktisch nie.
Оцените, пожалуйста статью